杆臂效应问题及相关探讨

主、子惯导由于安装位置的不同，感受的比力会不同，从而导致杆臂效应，在利用主惯导信息进行标定时必须消除杆臂效应的影响。对杆臂效应进行处理主要有两种方法：第一种方法，不对主、子惯导的输出速度之差进行处理，而在建立的卡尔曼滤波器系统动态方程中考虑杆臂效应，给出系统杆臂速度的微分方程，设计卡尔曼滤波器，同时估计杆臂效应速度和其他所需的参数。第二种方法，设计卡尔曼滤波器时，在系统动态方程中不考虑杆臂效应带来的影响，而在观测量中对杆臂效应引起的额外的速度误差量进行补偿，经过杆臂效应补偿以后，卡尔曼滤波器的观测量就能更加准确地反映出滤波器的系统模型。第一种方法增加了系统维数，增大了计算量，不利于在线标定。于是本书采用第二种方法。

在不考虑挠曲变形的前提下，当存在角运动时，主惯导感受的速度为

子惯导感受的速度为

则主、子惯导速度差为

在进行卡尔曼滤波时，速度误差观测量应改为

位置误差观测量应改为

其中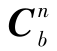，为子惯导的方向余弦矩阵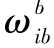；为主惯导感受的角速度；l为杆臂长度；L为当地纬度；RM、RN分别为地球子午圈和卯酉圈半径。(www.xing528.com)

1.主、子惯导之间姿态矩阵的关系

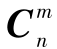由于安装误差，子惯导相对主惯导存在姿态误差，两者之间的初始姿态转换矩阵为，则主、子惯导相对n系的姿态矩阵和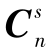之间的关系为

2.主、子惯导之间加速度的关系

由于杆臂效应的存在，主、子惯导感受不同的加速度。

主、子惯导之间加速度的关系为

其中，abm为主惯导感受的加速度；abs为子惯导感受的加速度。