惯导标定技术的发展现状和优化探究

1.可观测度分析方法

从计算原理上可以看出，惯性导航系统属于时变系统。对时变系统进行误差估计前，有必要分析系统中各待标定参数的可观测性，从而为滤波估计结果的预测、载体机动路径的设计提供理论依据。针对这一问题，Ham［5］给出一种可观测度定义，通过计算状态方程估计误差协方差阵的特征值和特征向量来确定系统的可观测度，最后推算出系统的可观测度与估计误差协方差阵的特征值成反比。东南大学的万德钧等［6］研究了系统可观测矩阵的奇异值分解，用得到的奇异值大小表示状态量的可观测度。Wu等［7］通过设计双轴旋转方案研究初始对准中的可观测性问题，证明了惯导系统三轴向零偏都可观测，但是该方案在标定中难以实现。Hong等和Tang等［8-9］推导了载体机动方式与系统中各误差参数可观测度之间的关系，但是其在推导过程中只考虑了以位置误差作为观测量，在实际应用中有较大的局限性。Dissanayake等［10］将“非完整性约束”理论引入惯导系统的可观测性分析中，利用该理论推导了系统各误差参数的可观测度，效果较好。杨晓霞和黄一［11-12］针对惯导系统的可观测性问题进行了深入研究，比较分析了各误差参数的估计收敛速度，并理论推导了天向陀螺零偏可观测性较差的原因，同时还将扩张状态观测器（extended state observer，ESO）和跟踪微分器（tracking differentiator，TD）应用到标定过程中，提高了误差标定的精度。

当前对惯导系统的研究中，基于分段线性定常系统（piece-wise constant system，PWCS）的可观测性分析方法和基于奇异值分解（singular value decomposition，SVD）的可观测度分析方法是最常用的两种分析方法。

对线性时不变（linear time-invariant，LTI）系统进行可观测性分析时，可直接通过计算可观测矩阵的秩来判断系统是否完全可观测。对于时变系统的可观测性分析，则需要求出系统的格莱姆矩阵［13］，而格莱姆矩阵的求取只能通过数值计算的方式，对于一些维数稍高的系统而言，计算量巨大并且无法进行理论分析。为了解决这一问题，以色列学者Goshen-Meskin和Bar-Itzhack［14-15］提出了PWCS可观测性分析方法，其原理是将时变系统划分为多个时间段，在不改变系统原有的特性的前提下将每一个时间段等效为线性定常系统来处理，这种方法虽然解决了系统的时变问题，但只能定性地分析系统整体的可观测性，无法分析某一个状态量独立的可观测性以及定量地计算系统的可观测度。

目前在实际工程中应用较为广泛的是由赵睿、程向红等［16-17］提出的基于SVD分解的可观测度分析方法，其本质是把系统可观测矩阵的奇异值定义为系统的可观测度，采用该方法无须计算估计方差矩阵，通过计算得出可观测矩阵的奇异值大小与系统的可观测度成正比。基于SVD可观测度分析方法，孔星炜等［18］提出了相对可观测度和可观测阶数的概念，以此来分析系统的可观测性，并进行了车载试验验证，得到的试验结果与理论研究相吻合。刘准等［19］将条件数理论引入可观测度分析中，利用条件数定义整个系统的可观测度，该方法既能够定量分析时不变系统的可观测性，又能够定量分析时变系统在任意时间段内的可观测性，实际应用性较强。然而，马艳红等［20］对SVD方法的实用性进行了研究，认为在采用该方法比较不同状态量可观测度大小时，需要利用变量代换法对状态量进行无量纲化处理，但是在变换前后可观测度结果会发生变化，他们通过几个实例证明了SVD方法存在一定理论缺陷。

2.匹配模式

针对捷联惯导系统而言，对惯性器件误差的标定和补偿技术是提高其导航精度的重要手段，而匹配模式的选择是影响标定效果的重要因素。卡尔曼滤波器的观测量是由主、子惯导的同类输出量做比较后形成的，根据所用观测信息的不同可得到在线标定的不同匹配模式。如果用主、子惯导的速度输出构造观测量，则称在线标定采用“速度”匹配模式；如果由主、子惯导的角速度输出构造观测信息，则称在线标定采用“角速度”匹配模式。目前常用的观测信息包括角速度、速度、位置等，其中速度匹配和位置匹配在国内外相关研究中，应用最为广泛，技术也最为成熟。近年来，在不同的条件下，几种匹配方案相结合的联合匹配方法逐渐发展成熟起来，它具有标定精度高、速度快的优点，代表着匹配模式的发展方向。

文献［21］采用“速度＋加速度＋姿态角＋角速率”联合匹配模式，能够标定出较多误差参数，但计算量巨大，最高达到了39维。文献［22］研究了捷联惯导系统在“速度＋姿态”匹配模式下的在线标定，但没有分析论证匹配模式的选择问题。文献［23］基于卡尔曼滤波算法及最小二乘理论，分别研究了速度加姿态匹配、角速度匹配、比力匹配模式下的弹载惯导标定效果，但没有分析不同匹配模式的优劣。文献［24］仿真分析了采用速度匹配模式时，失准角估计效果不理想，而采用速度加姿态匹配时，当载体进行特定机动时可有效提高系统的可观测性。因此，选择不同的匹配模式对在线标定效果影响很大，研究不同匹配模式下的在线标定对提高标定精度具有重要意义。

3.误差激励(www.xing528.com)

误差激励方式的不同直接影响着状态变量可观测度。文献［25］为了能够激励惯性器件全部12个误差参数，设计了载体做匀速圆周运动的同时做横滚及偏航运动，但是其所设计的机动方式过于复杂，工程实用性不强。文献［26］和文献［27］为了标定出惯性器件的刻度系数误差、零偏及安装误差等全部24个误差参数，设计了载体静止与转动相结合的机动方式，且标定过程中以比力输出值在地理系中的投影作为观测量，但是其标定精度易受基座扰动干扰，且转动过程也比较复杂。文献［28］充分利用船体在海水作用下轻微的俯仰、偏航及横滚机动，以GPS外测信息为基准完成对船载惯导系统的在线标定，但是由于机动角度较小，标定精度一般。彭靖等［29］采用“速度＋姿态”匹配模式，研究了四种不同机动方式下捷联惯导系统误差的激励效果，在综合考虑传递对准效率及精度的前提下得出了最优的机动方式。国防科技大学的吴文启教授等［30］通过安装一个30°的斜面来激励误差参数，且对惯导系统的特点进行了研究，提出以惯导系统水平姿态修正量与重力测量结果作为观测量，完成对器件误差的标定。Pittman等［31］通过设计一种安装惯性器件的环架机构，使惯性器件完成固定角度的转动，从而估计出对准失准角及器件零偏。文献［32］和文献［33］将环境函数法用于惯导误差的分离，在对器件误差进行辨识时仅需以速度作为观测量即可辨识器件误差，但环境函数矩阵在计算过程中存在较大的线性化误差，矩阵的计算和推导都十分困难。总之，研究切合实际的机动方式以充分激励惯性器件误差参数是下一步研究的重点。

4.噪声统计特性不确定情况下的滤波方法

卡尔曼滤波是一种递推估计的滤波算法，它基于状态空间模型，估计的最优准则是最小均方误差，适用于实时处理和计算机运算［34-35］。

卡尔曼滤波算法在各类工程实际中被广泛应用，但是其限制条件也十分严格：一是系统必须是线性的且模型的参数准确已知。二是系统中的状态噪声和观测噪声必须是零均值高斯白噪声。三是状态噪声及观测噪声的统计特性必须是精确已知的。为了消除卡尔曼滤波在使用过程中的条件限制，很多专家进行了大量的研究。针对条件一，一些专家学者提出了能够适用于非线性系统的滤波算法，如无迹卡尔曼滤波（UKF）、容积卡尔曼滤波（CKF）以及扩展卡尔曼滤波（EKF）等，而鲁棒滤波（H 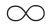）和自校正滤波解决了模型参数不确定的问题。针对条件二，一些专家学者提出了粒子滤波（PF），它可以通过粒子模拟噪声分步完成最优估计。针对条件三，为了保证滤波的最优性，一些专家学者提出了自适应卡尔曼滤波（AKF）、强跟踪卡尔曼滤波（STKF）、多模型卡尔曼滤波（MMKF）以及Sage-Husa滤波。考虑到多管火箭武器系统在线标定的野战环境比较恶劣，噪声的先验统计特性无法精确获得，会严重影响滤波的效果，因此研究噪声统计特性未知的情况下如何保证滤波的效果十分必要。

针对上述问题，前人在标准卡尔曼滤波算法的基础上提出了几种改进滤波算法，如Bryson等和邓自立［36-37］分别针对系统噪声不符合互不相关假设和零均值假设而提出了增广卡尔曼滤波算法；Li等、Mehra和Xing等及付梦印等［38-41］针对系统噪声协方差矩阵信息不完全已知而提出了自适应卡尔曼滤波算法。但是，以上研究中状态维数增高的同时计算量也成倍增加，且估计效果也没有得到理论证明。

自适应滤波是将自适应控制的思想应用到滤波估计问题中，对未知的状态噪声协方差矩阵和观测噪声协方差矩阵进行实时估计。自适应滤波算法的研究中，Sage-Husa自适应滤波算法是较早被提出来的，但是该方法在应用中容易出现滤波发散，且方差的正定性无法保证，进而可能导致滤波无法继续进行，而且其中的协方差矩阵的估计也被证明是有偏估计。针对Sage-Husa自适应滤波算法存在的这些问题，很多专家学者进行了深入研究，提出了一些改进算法。王忠等［42］通过引入渐消因子改善滤波器的动态性能并应用到GPS／INS（惯性导航系统）组合导航中。在王忠等研究的基础上，范科等［43］进一步发展了该方法，将算法中的单一遗忘因子替换为多遗忘因子，提高了算法的自适应性。同时，为了限制滤波的发散，鲁平等［44］在Sage-Husa自适应滤波算法中加入阈值的限制。黄晓瑞等［45］以新息和观测信息的吻合程度作为指标，提出一种使系统在Sage-Husa自适应滤波和强跟踪自适应滤波之间能够随意切换的算法。针对Q、R矩阵非正定性问题，魏伟等［46］对Sage-Husa自适应滤波进行了改进，强化了系统初值的作用，仿真效果较好。以上方法虽然不同程度上提高了滤波的效果，但是没有从根本上解决滤波发散的问题。

此外，很多学者还提出了新的自适应滤波算法。魏燕明［47］详细推导了基于大数定律的三种不同估计形式（只估计Q阵，只估计R阵，同时估计Q、R阵）下的计算公式。王跃钢等［48］为了抑制噪声方差发散对滤波过程的影响，将模糊判断思想加入自适应滤波中，在自适应因子的选取中加入了模糊判别。高为广等［49］将神经网络加入自适应滤波中，用神经网络修正状态量预测，可有效抑制扰动异常带来的影响。汪坤等［50］采用低通滤波器对信号进行预处理，降低了噪声在信号中的比重，有利于后面滤波的进行，取得了很好的效果。上述方法都是基于大数定律的思想，将包含待估计噪声的项单独分离出来，利用大数定律求取该项的方差对待估计项进行近似，但是这种方法会破坏滤波回路及增益计算回路的独立性，使滤波的优越性和稳定性无法得到保证。

除了基于大数定律的自适应滤波算法外，何秀凤等［51-52］提出了扩展卡尔曼滤波，将滤波的误差限定在一个已知的区间内。杨长林等［53］进一步发展了该方法，通过滤波新息来估计噪声方差，提高了滤波的鲁棒性。