M指标的思想方法与计量框架简介

在Wigner（1959）的基础上，在生态系统中的稳定性和复杂性关系研究中，May（1972）分析了变量数目很大的复杂巨系统，在极限情况下从稳定性突然向不稳定转变的临界点情况。假设系统包含n个变量，比如生态系统中的变量是相互作用的物种，这些变量服从非线性的一阶微分方程。当该系统达到均衡时，稳定性可以写成

其中，在一个生态系统中，x是相互作用的物种xj（j=1，2，…n）构成的n×1阶列向量。A是n×n阶相互作用矩阵，A中的元素ajk表示系统达到均衡时物种k对物种j的影响。由营养网络结构图分析可知，当没有网络连接时，ajk=0；且物种之间相互作用的类型决定了ajk的大小和正负号。

May（1972）假设每一个物种本身都具有密度依赖或其他的稳定形式，因此，当均衡受到扰动时，它将以某种特定的衰减时间回归均衡。为设定一个时间尺度，May将该衰减时间归一化，即a jj=-1。随后，物种间的相互作用“开启”，且假定每一个这样相互作用的单位是等可能地为正或负，其绝对值由某个统计分布给定。为简单起见，May（1972）假定矩阵中的每一个元素都服从均值为0和均方差α的随机分布，α可视为平均相互作用强度，简单地说：

其中，B是一个随机矩阵，I是一个单位矩阵。这样，我们得到一个无标度的模型，每一个相互作用矩阵单位的特定选择都可以独立地从随机分布中导出。经过比较复杂的推导，May（1972）提出了May-Wigner稳定性定理。

May-Wigner稳定性定理：假设矩阵B是一个具有n2C（0＜C＜1）个随机分布非零项的n×n阶的矩阵，其中的每一个元素均独立的方差为α2的对称分布。P（α，n，C）是使得式（6.1）在0处达到均衡时的概率水平。令微小常数ε＞0，随着n→∞，如果α2n C＜1-ε，则有P（α，n，C）→1-ε；反之，随着n→∞，如果α2nC＞1-ε，那么P（α，n，C）→0。

这一定理是生态学中的复杂巨系统达到均衡时系统稳定性的基础，并且指出了系统由稳定向不稳定转变的临界水平。Mayet al.（2008）将该定理应用到银行生态系统的研究之中，Heiberger（2014）则进一步将该定理应用于股票市场网络研究，提出了股票市场系统稳定性计量的m指标。本章将应用该指标研究中国资本市场（以股票市场为代表）的系统稳定性。

为了计量m指标，我们需要构建一个合适的股票网络。从股票交易的真实数据，如股票的收盘价、收益率或交易量，股票网络将每个股票视为一个结点（node），股票与股票之间的相关关系视为连接（link）或边（edge），相关系数是边的权重，股票市场中的所有股票及其相关关系构成一个股票网络。

假设两只股票i和j，如果股票i的价格变动引起股票j的价格变动，则它们之间的影响关系由i指向j。反之，它们的影响关系由j指向i。假设股票i在某一时刻t的价格为Pi（t），Ri（t）表示股票i在该时刻的对数收益率，即

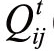（τ）表示在t时刻股票i在时间窗τ内对股票j的相关系数，计算公式为

其中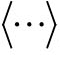，为统计平均，即

通过计算，可得到任意两只股票之间的相关系数而得到一个相关系数矩阵Qt（τ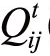）=（（τ））N×N。

分析相关系数矩阵的取值，可知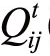（τ）的值在-1和1之间，即-1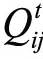＜（τ）＜1。如果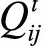（τ）＞0，说明股票i对股票j的影响为正，股票j的价格会向着股票i价格变动的方向波动。如果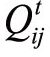（τ）＜0，则股票i对股票j的影响为负，股票j的价格波动方向与股票i价格变动方向恰好相反。如果|，则认为股票i和j的相互影响关系是从j流向i，在股票网络上即意味着一条从节点j到节点的有向边。如果|，则认为股票i和j的相互影响关系是从i流向j，在股票网络上建立一条从节点i到节点j的有向边。如果，说明股票i和j之间的影响是对等的，在有向网络中没有连边。(www.xing528.com)

为了缩减股票网络的规模，需要利用某个阈值来选取股票之间的连边。这里，我们采用Tse et al.（2010）的“赢者通吃（winner-take-all）”方法，边的选择准则是股票之间的相关系数只有当高于某个阈值时才被选择。那么，在某个时刻t股票网络的选择准则为

相比于其他的缩减技术，这样的选择准则具有两个优点：一是确保股票网络不会丢失重要的信息，如果高相关性的节点落在被缩减的图形内，最小生成树和平面图方法会移除连边，以使连边自适应网络的拓扑条件；二是股票网络中的节点数不是事先确定的，即没有固定的上限，这对于生态类比和May-Wigner稳定性定理是特别重要的。

其次，根据May-Wigner稳定性定理，股票网络达到稳定的条件是

其中，n是股票网络的规模，是网络中的股票数量；a是网络中的平均相关系数，即股票网络中所有相关系数的平均值；C是股票网络的聚集系数，反映了股票网络中节点聚集程度。具体来说，假设股票网络中的某个节点i有ki条边与之相连，则这ki条边对应的ki个节点均称为它的邻居节点。显然，在这ki个节点之间最多只可能有ki（ki-1）/2条边，而实际上在这ki个节点之间存在的边数为Ei。那么，节点i的聚集系数被定义为与之相连的邻居节点之间实际存在的边数Ei与所有可能存在边数的比值，即Ci=2Ei/［ki（ki-1］。同理，股票网络的聚集系数C就是所有节点i的聚集系数的平均值，即

式（6.7）是对已知的生态多样性和稳定性之间关系的挑战。May（1972）认为，当网络连接过于丰富（即nC太大）或平均相互作用强度过于大（即a太大）时，都会导致生态系统的不稳定。May（1972）也可以从另一个角度来解释复杂性和稳定性之间的关系，增加网络的复杂性，会降低系统的稳定性。这种关系广泛存在于生态网络、小世界网络以及动态网络之中，这对于我们研究现实中的股票网络也非常重要。

由May-Wigner稳定性定理可知，m值的大小能够很好地度量股票市场系统稳定性。因此，我们将该指标定义为m指标，即m=。通过上述分析，我们可以确定m指标计算的基本步骤如下：

（1）选择成分股。构造股票网络时，最基本的问题是成分股的选择。基于股票交易连续性的考量，剔除连续若干个月停牌交易的股票，选择了上证综指的274只成分股作为来构造股票网络，样本期间为2005年2月1日—2016年8月31日，共有2 676个交易日，采用股票的每日收盘价计算对数收益率数。数据收集自国泰安（CSMAR）股票市场数据库。并且，计算这274个股票每月的平均收盘价（Average Closing Price，即ACP）作为上证综指的替代指数。

（2）设置时间窗。为了研究股票市场系统稳定性的动态特征，我们将所有274只股票所构成的数据集划分为M个月，定义为t=1，2，…，M，每个月的时间窗宽度为τ（即在每一时间窗内的每日收益率数量）。时间窗部分重叠，将以δ τ的长度向前移动，δτ设置为1个月内的交易日，通常取一个月有21个交易日，这符合Onnela（2003）所提供的选取标准。通过比较不同时间窗口下的分析结果，本章选择结果是1年的窗口（即τ=250），δτ=21，整个样本期内共有128（2676/21）个月。

（3）计算相关系数。根据式（6.4）的计算，我们可以得到在时间窗τ内股票i和j的相关系数（τ）和相关系数矩阵Qt（τ）=，以及N（N-1）/2个相关系数。

（4）设定阈值z。股票网络的构建离不开阈值z的设定，不同的阈值选择的股票之间的边（edge）数量不同，在分析股票网络的拓扑性质时也会发生偏差。吴翎燕、韩华和宋宁宁（2013）认为当阈值为0.657时，股票网络的拓扑性质最稳定。因此，我们将z设定为0.657，构建z=0.657下的股票网络。

（5）计算m指标。在第t月内，通过构造股票网络，我们可以得到股票网络的一些参数，如股票网络中的股票数量n、平均聚集系数C和平均相关系数a，进而根据式（6.7）计算在该时间窗内的m指标数值。通过变动月份t的取值，我们可以得到一系列的m指标值。