实证研究的前期准备步骤

1.实证研究模型

首先选用VAR估计主板、中小板、创业板之间的收益率溢出效应，而后基于VAR的残差，用DCC-GARCH来估计主板、中小板、创业板的动态相关性。VAR设定如下：

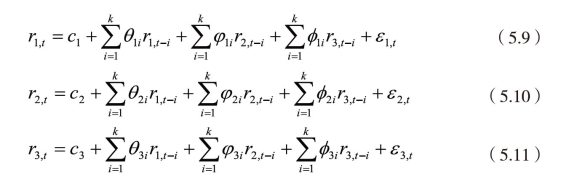
其中，i=1，2，r1，t、r2，t、r3，t分别为主板、中小板、创业板在t期的收益率，c1、c2、c3是常数项，θ、φ、φ是滞后期的系数估计，ε为残差项。

θ表示主板收益率的滞后期对主板、中小板、创业板收益率当期的影响；φ表示中小板收益率的滞后期对主板、中小板、创业板收益率当期的影响；φ表示创业板收益率的滞后期对主板、中小板、创业板收益率当期的影响此时。可通过θ、φ、φ的大小和显著性来判断板块间的收益率溢出。当VAR模型是稳定的，即建立的VAR模型的特征根均在单位圆内，可以进行格兰杰因果检验，以进一步分析主板、中小板、创业板收益率之间的动态关系，检验他们是否存在时间上的先导—滞后关系，即进一步确认板块间的收益率溢出情况。

Engel（2002）提出的DCC-GARC模型为研究金融市场间的动态相关系数提供了方法，能更好地刻画板块间的动态相关变化，尤其有助于分析研究在不同市场行情下的两者关系。最初的DCC-GARCH是基于收益率为联合正态分布假设估进行估计，为了提高模型的适用性，可从两方面改进DCC-GARCH，第一是假设联合正态分布为T分布，第二是假设波动率模型存在杠杆效应。本章先采用基于T分布的DCCGARCH模型来估计板块收益率之间的动态相关系数。

DCC-GARCH需通过两个步骤来估计两市之间的动态相关系数。首先，利用GARCH模型分别估计出股市、债市收益率的条件方差，并计算得到标准化残差序列，然后将标准化残差序列代入DCC动态结构模型中，采用极大似然法估计动态结构模型的参数，得到动态相关系数矩阵。

模型表述如下：假设k种资产收益率rt的随机项ε t服从均值为0，协方差矩阵为Ht的多元T分布，即εt|It～T（0，Ht，v），It是0到t-1期的信息集。

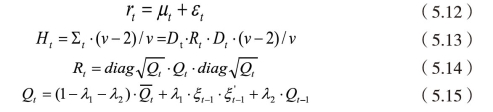
其中，Dt是k*k维度的动态标准差矩阵，是由给资产收益率方差构成的对角矩阵，Rt是动态条件相关系数矩阵，即

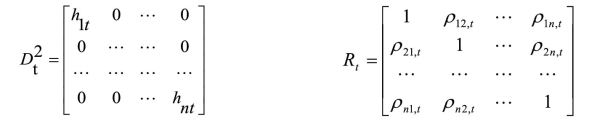
其中，hit是单变量GARCH估计出的条件方差，ρit是资产i、j在t时的相关系数。Qt为εt的条件协方差矩阵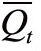，是无条件协方差矩阵；ξt是标准化的残差序列，即ξt-1=εt-1·Dt-1-1，λ1，λ2为非负参数，且λ1+λ2＜1保证标准化后的残差项的条件协方差矩阵正定并满足均值回复这一条件。当λ1=λ2=0时，DCC模型退化为CCC模型，即板块间的相关系数是常数。

采用极大似然法对DCC-GARCH模型以联立形式估计，DCC估计式中包括板块收益率及其标准化残差的GARCH（1，1）过程，并对股市、债市的标准化残差项进行自相关检验以保证模型拟合的充分性。模型估计采用OxMetrics软件。

2.研究样本与描述性统计(www.xing528.com)

选取沪深300指数、中小板指数、创业板指数计算主板、中小板、创业板的收益率。沪深300指数由沪深两市主板市场中规模、流动性排序前300的股票加权而得，基期为2004年12月31日，于2005年4月8日正式发布。中小板指数选取的是中小板市场规模和流动性前100的股票加权而得，基期为2005年6月7日。创业板指数选取的是创业板市场规模和流动性前100的股票加权而得，于2010年6月1日正式开始编制和发布。因此，样本期间从2010年6月1日到2016年6月30日，共计1 447个数据。数据来源为Wind金融终端。指数收益率根据式（5.7）计算。表5-11列出了主板、中小板、创业板收益率的统计性描述。

表5-11　主板、中小板、创业板收益率的描述性统计

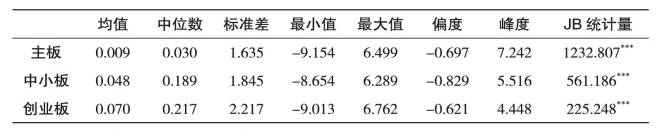
注：★★★表示在1%的水平内显著。

对比分析可知，主板、中小板、创业板收益率具有以下特征：①主板收益率均值、标准差、中值都小于中小板、创业板，创业板最高，体现了金融市场高风险、高收益的特征；②在最大值、最小值上，板块间并没有明显差异，板块收益率的偏度都为负，具有较长的左尾分布，说明各板块收益率会频繁地出现负收益或一些极大的损失；③JB统计量表明，主板、中小板、创业板收益率序列都不是标准的正态分布，且主板收益率有着更强的尖峰特征，说明主板收益率更多地分布在均值和尾部区域，出现偏离均值的极端收益率的可能性更大。

图5-5是主板、中小板、创业板的收益率走势图，上述特征也可以从收益率走势图中看出。此外，相比之下，2015年之前收益率走势相对平稳，2015年之后，收益率波动更为剧烈，其中创业板波动最大。

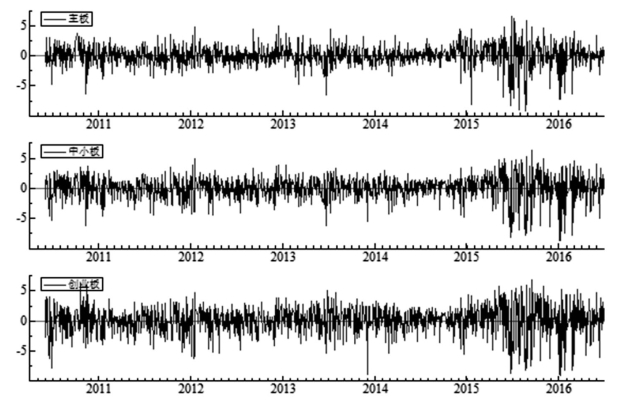
图5-5　板块收益率时序图

为了避免伪回归问题，在模型估计前对板块收益率进行平稳性检验。采用ADF检验对收益率序列进行单位根检验，采取无趋势项、无常数项形式，结果表明板块收益率序列在1%的显著性水平内平稳。结果见表5-12。

表5-1 2　收益率的平稳性、自相关性、ARCH效应检验

注：★★★表明在1%水平内显著；Q（20）、Q2（20）分别是残差序列、残差序列平方Ljung-Box检验的Q统计量。

金融资产收益率往往存在序列自相关。采用滞后20期的Ljung-Box Q统计量对板块收益率序列进行自相关检验。在1%的显著性水平内，均拒绝了不存在序列自相关的原假设，说明收益率存在显著的自相关性。

收益率序列的ARCH效应检验有两种方法：一种是检验均值方程中残差序列平方的自相关性；另一种是对收益率序列进行ARCH-LM检验。由表5-12的Q2（20）统计量可知，残差中存在ARCH效应，滞后5阶和滞后10阶ARCH-LM检验也得到了同样的结果。