股指崩盘与跳跃的Logistic回归探究

本章首先讨论系统稳定性对股指收益率崩盘或跳跃概率的影响。对于股指收益率而言，因为无法计算其简单超额收益与Jensen's alpha超额收益率，所以，股指崩盘与跳跃事件的识别仅使用其原始收益率。

表4-4为股指收益率崩盘的Logistic回归结果。在最初的回归中，模型自变量仅包含系统稳定性指标，为了说明系统稳定性指标包含比一般波动性更多的信息，本章进一步将波动性纳入模型自变量，其中，股指收益率的波动性被计算为日收益率在当月的标准差。

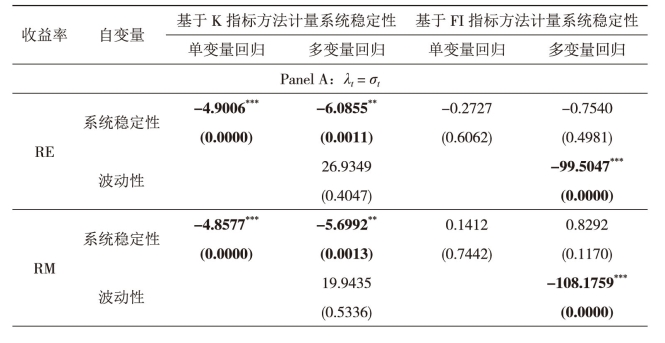
表4-4　股指收益率崩盘的Logistic回归

续表

注：括号内为p值，★，★★，★★★分别代表p值小于0.1、0.05、0.001，字体加粗表示在90%的水平上显著不为零。(www.xing528.com)

表4-4第一列说明了用以计量系统稳定性的收益率序列。在Panel A与Panel B中，崩盘分别被定义为当期收益率低于收益率均值一倍与两倍标准差的情形。表4-4比较了基于K指标方法与基于FI指标方法计量的系统稳定性对股指收益率崩盘概率的影响。通过进行单变量回归可以发现，在各收益率情形与崩盘识别标准下，基于K指标方法计量的系统稳定性均负向显著影响股指崩盘概率，说明，系统稳定性程度越强，股指崩盘的概率越低；相反，基于FI指标方法计量的系统稳定性的影响则均不显著。

进一步加入波动性指标后，基于K指标方法计量的系统稳定性依然显著影响股指崩盘概率，而波动性则并不显著，这说明系统稳定性包含了比波动性更为丰富的信息。相比之下，在大部分情形下，基于FI指标方法计量的系统稳定则不能显著影响股指崩盘概率。

表4-5是股指收益率跳跃的Logistic回归结果，其中，Panel A与Panel B分别将跳

跃定义为当期收益率高于收益率均值一倍与两倍标准差的情形。可以发现，在单变量与多变量回归中，基于FI指标方法计量的系统稳定性均不能显著影响股指跳跃概率。相比之下，基于K指标方法计量的系统稳定性在单变量回归中均显著负向影响股指跳跃概率。但是，在自变量加入波动性指标之后，基于K指标方法计量的系统稳定性的显著性程度出现明显下降。这与表4-4的结果出现了一定程度的偏离，反映了市场波动的非对称性，即市场波动对下跌的反应比对市场上升的反应更加强烈。

表4-5　股指收益率跳跃的Logistic回归

注：括号内为p值，★，★★，★★★分别代表p值小于0.1、0.05、0.001，字体加粗表示在90%的水平上显著不为零。