崩盘与跳跃状态的识别及优化措施

参考Marin & Oliver（2006）、李志生等（2015）的研究，本章使用以下标准识别资产价格崩盘与跳跃事件，并分别记为二元虚拟变量DC，t与DJ，t。当资产j第t月的收益率相对收益率均值出现大幅下降时，则认为资产价格出现崩盘事件，记DC，t=1，否则DC，t=0；类似地，当资产j第t月的收益率相对收益率均值出现大幅上升时，则认为资产价格出现跳跃事件，记DJ，t=1，否则DJ，t=0。

具体以简单超额收益率RE为例，本章通过以下方式识别资产价格崩盘事件：

并将资产价格跳跃事件定义为

在以上两式中，为前36个月的简单超额收益率移动均值，λ t用于界定巨幅上涨或下跌，本章考虑了一倍的移动标准差与两倍的移动标准差两种情形。类似地，在以原始收益率RW与Jensen's α超额收益率为对象的研究中，本章采用一致的方法识别崩盘与泡沫事件。

进一步地，本章的Logistic模型统一采用以下设定：用D t统一指代DC，t或DJ，t，假设存在潜变量与随机变量D t之间具有一一对应的映射关系：当大于临界值c时，Dt=1；当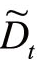不小于临界值c时，Dt=0，即

假设潜变量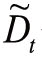与自变量具有线性关系，可以用回归模型的方式表示，即(www.xing528.com)

其中，Xj，t为第j个自变量在t的观测，βj为相应的回归系数，ui，t是相互独立、均值为0的随机扰动项，其服从逻辑分布。

在这一设定下，崩盘或跳跃事件的发生概率为：

其中，F是逻辑分布函数。对上式求关于自变量xj，t的偏导，可得：

其中，f是逻辑分布的密度函数。根据上式，崩盘或跳跃概率随自变量xj，t变动的方向与回归系数βj的符号一致。