基于主成分分析的系统性风险暴露度量优化

本章从行业的视角计量中国股票市场的系统稳定性，这不仅因为行业收益率可以通过行业指数直接计算获得，可以简化研究步骤，还因为行业特征是投资者进行投资决策的重要考量因素。研究使用在理论研究与实务工作中被广泛应用的申万一级行业分类，这一分类标准将中国股票市场分为28个行业，行业指数数据来自Wind金融终端中2002年1月至2016年7月的日度数据。

为了得到稳健的结论，本章分别计算了简单超额收益、Jensen's alpha两种超额收益率，并使用相应收益率序列计量系统性风险暴露与系统稳定性。其中，行业j在t期的原始收益率RWj，t为

其中，Pj，t是行业j在t期的收盘价；相应地，简单超额收益率REj，t被计算为

其中，是市场指数收益率，其基于申万股票指数以与式（4.12）一致的方法计算得到；Jensen's alpha超额收益率RMj，t被计算为(www.xing528.com)

其中，Rf，t为无风险收益率，本章使用1年期的SHIBOR利率作为代理变量。

Berger & Pukthuanthong（2016）将FI指标方法用于考察股票市场的系统稳定性。参考其研究，本章按照月度频率计量系统性风险暴露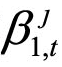，即使用日度收益率观测数据根据式（4.1）逐月回归。基于式（4.1），针对每一个行业，为了计量其系统性风险暴露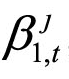，需要首先求解行业收益率的主成分。在主成分分析中，Berger &Pukthuanthong（2016）分别全样本与滚动样本计算协方差矩阵，并发现前者基本消除了系统性风险暴露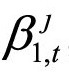的动态性特征。因此，在计算第t月主成分时，本章滚动地使用其前12个月的日度收益率计算协方差矩阵。

图4-1为各主成分对收益率样本方差的累积贡献率。从图4-1可以发现，对简单超额收益率与基于Jensen's alpha的超额收益率而言，前20个主成分的累积贡献率超过90%，换句话说，前20个主成分至少可以解释90%以上的样本方差。因此，本章选择前20个主成分作为回归自变量。

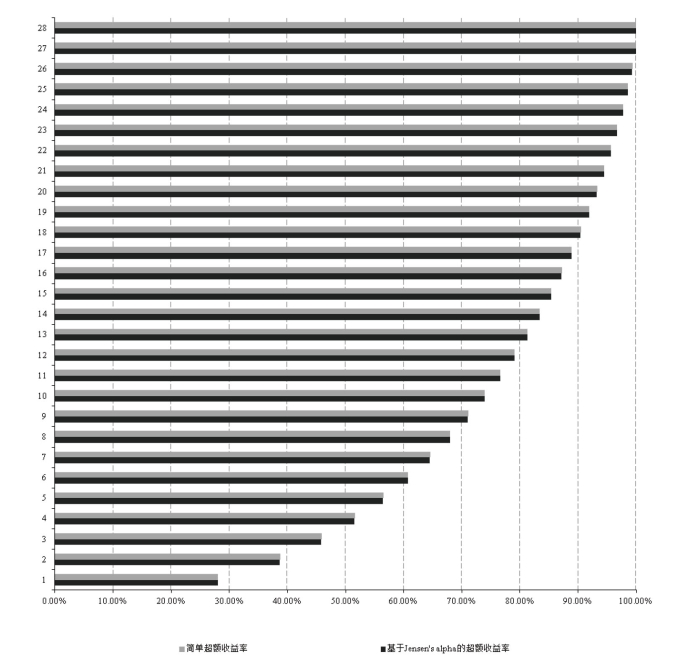
图4-1　主成分累计贡献率