【摘要】：为了行文方便，下文称之为K指标。由于无法被直接观测，因此，也无法被直接观测，可以假设其中，μe=，εe，t为扰动项，服从正态分布N。记Vt=ln［kt/］，并假设系统稳定性将随着时间动态变化，其服从AR过程：其中，扰动项目εV，t为扰动项，服从正态分布N。至此，（4.8）、（4.9）与共同组成了一个标准的状态空间模型，其中，式（4.8）与（4.9）共同构成了状态空间模型的量测方程，式为状态空间模型的状态方程。
假设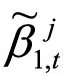
为系统性风险暴露在t期的均衡值，定义投资者对系统性风险暴露的定价偏差为
在横截断面维度，以下关系成立：
的
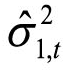则为系统稳定性程度越高，系统性风险暴露的定价偏差越低，
因此，本章使用两者的接近程度作为计量系统稳定性的标准，即定义指标
则kt将在［0，1］区间内变动，kt取值越大，系统性风险暴露的定价偏差越低，系统稳定性程度越高。为了行文方便，下文称之为K指标。
根据上述可得式（4.7），两边取对数为式（4.8）。(www.xing528.com)
由于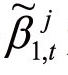
无法被直接观测，因此，
也无法被直接观测，可以假设
其中，μe=
，εe，t为扰动项，服从正态分布N（0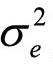
）。
记Vt=ln［kt/（1-kt）］，并假设系统稳定性将随着时间动态变化，其服从AR（1）过程：
其中，扰动项目εV，t为扰动项，服从正态分布N（0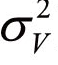
）。至此，（4.8）、（4.9）与（4.10）共同组成了一个标准的状态空间模型，其中，式（4.8）与（4.9）共同构成了状态空间模型的量测方程，式（4.10）为状态空间模型的状态方程。因此，在使用Kalman滤波方法估计出Vt序列后，K指标被计算为
因此，K指标在（0，1）区间范围内。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
