羊群行为视角下的股票市场系统稳定性评估思想方法

尽管Pukthuanthong & Roll（2009）并没有专门讨论系统稳定性的计量，但其对全球金融市场一体化程度的分析，为系统稳定性计量提供了一个有用的框架。在对多个金融市场收益率进行样本外主成分分析的基础之上，Pukthuanthong & Roll（2009）提供的经验证据表明，主成分分析可以有效反映潜在的全局性因素。因此，其将各金融市场收益率对多个主成分进行回归分析，即

其中，Rj，t是第j个金融市场的超额收益率，PCi，t是第i个主成分，是相应的回归系数，ej，t是回归残差项，回归方程的R2值则被用于计量金融市场一体化的程度。

基于这一框架，Berger & Pukthuanthong（2012）提出了国际金融市场的系统稳定性测度方法，其认为第一主成分最好地刻画了全局性因素，也对全球金融市场波动的贡献率最大。回归方程式（4.1）中对第一主成分的回归系数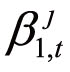代表了金融市场j对于全局性因素的风险暴露。当全球金融市场平均暴露程度较高时，全局性因素的负面冲击容易引发导致全球金融市场的系统性危机，因此，其使用的横截面平均值计量全球金融市场的系统性风险，即FI指标。

尽管Berger & Pukthuanthong的实证结果表明，FI指标对于预测全球金融风险的崩盘与跳跃风险具有良好的表现，但该指标也存在以下不足。

首先，比较式（4.1）与CAPM模型可以发现两者具有类似的结构，也具有与CAPM模型下贝塔值类似的性质。与CAPM模型不同，式（4.1）中被允许动态变化的，而CAPM模型中的贝塔值是静态的，不随时间改变。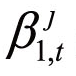的动态变化既可能由不完全信息、投资者的非理性行为等市场摩擦因素导致，也可能是资产内在价值变动引起，而后者是市场有效率的体现，不应纳入系统性风险的范畴，前者将导致对系统性风险暴露的定价偏离均衡值，催生资产价格泡沫与崩盘，从而增大系统性风险。(www.xing528.com)

其次，作为算数平均值，FI指标将不可避免地会受到极端值的影响，而且如果不服从正态分布，那么FI指标将不具备样本代表性，而无法正确反映系统性风险的大小。相比之下，暴涨暴跌是系统不稳定的主要表现形式。因此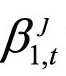，在横截面上的二阶矩特征比算术平均值这一阶矩特征更能表征市场的系统性风险。

从形成机制而言，投资者的羊群行为与资本市场系统稳定性均强调了个体之间的传染性特征。羊群行为反映了投资者行为之间的相互学习与模仿，而资本市场系统稳定性则强调了资产价格之间的高度相关。

目前，羊群行为的计量主要包括两类思路，一类是根据投资者的持仓数据，直接考察投资者的交易行为，另一类则直接考察资产价格波动的一致性。相比之下，前者受制于数据可得性，只能考察季度甚至年度等较低频率的羊群行为，而且会受到投资者“窗装效应”的影响。

基于第二类研究思路，Hwang & Salmon（2004）在CAPM模型框架下提出了羊群行为估计的状态空间模型。由于CAPM框架与式（4.1）框架结构类似，因此，本章将重点参考其研究方法，构建资本市场系统稳定性的计量方法。