证券市场线和β值的关系及风险度测量

在资本市场线内容中，已经说明了所有有效证券组合都落在射线上，反过来，凡是非有效证券组合都处于有效边界的下方。这就需要进一步完善风险测度指标，否则，就无法合理地衡量非有效证券组合的风险与收益的关系。在本章第一节中，已经提到证券投资风险可分为系统性风险和非系统性风险。风险程度通过证券收益率概率分布的均方差来表示。证券组合可有效消除非系统性风险，即人们最终追求在无法避免的系统性风险情况下，投资效益达到最大化程度。换句话说，人们的证券组合总风险就是它所承担的系统风险，以弄清系统风险的方差VAR与预期收益率之间的关系。这里，引进β系数概念，所谓β系数，是美国经济学家威廉·夏普（William.Sharpe）提出的风险衡量指标，β系数是个相对指标，用它反映证券组合波动性与市场波动性的比，在一般情况下，将某个具有一定权威性的股指作为测量股票β值的基准，也称为市场组合。如果基准为1.0，而β值为1.1，即表明该股票波动性要比市场大盘高10％。同理，如β值为0.95，则说明该股票波动性弱于大势。它可较方便准确地反映投资收益与风险之间的关系。用β值衡量风险是利用统计学中的回归分析原理，世上事物都是相互联系和制约的，一个事物变动常受其他事物变动的影响。父母身高会影响孩子的身高，前者称为自变量，后者是应变量，孩子身高随父母而定，但父母身高不受孩子影响。统计学中利用回归分析法来观察两种以上互有联系的事物之间相互变动的关系。回归分析利用最小二乘法，其基本方程式为Y＝a＋bx，Y是应变量，x是自变量，a是Y的截距，也是回归系数。在证券投资中，人们利用β值代表某种证券受市场影响而产生价格波动的大小，达到测定其风险度的要求。把β值看成是用来测量某一证券利益对市场平均收益变动的敏感性指标。根据这一思路，人们采用回归方程式求得β值：Y＝a＋βx＋ε，Y为某证券预期收益率，a是纵轴回归截距，也是表示无风险资产利率，x为市场平均预期收益率，β为回归线的斜率，ε为剩余收益，由于随机差错因素而产生，理论上一般忽略不计。因为单个证券的价格波动与市场证券总体价格水平的波动不仅并不一直保持同步，甚至还会出现背离运动的倾向，所以以市场证券组合的平均收益波动为参照物，单个证券或证券组合的波动——风险也就相对容易衡量了。证券i的β值是相对于证券组合ρ而言，证券i收益的变动性。证券i的β值βiρ等于证券与证券组合ρ收益的协方差除以证券组合ρ的方差：

其中，

βiρ表示证券i相对于证券组合ρ的β值；

COViρ表示证券i与证券组合ρ收益之间的协方差；

Vρ表示证券组合ρ的方差。

证券组合Q的β值等于该证券组合中各证券β值的加权平均数，以各证券占证券组合Q的投资比重为权数：

式中，

βqρ表示证券组合q相对与证券组合ρ的β值；

Xiq表示证券i占证券组合q的投资比重；

βiρ表示证券i相对与证券组合ρ的β值；

n表示证券组合q中包含的证券数量。

β值越大的证券，预期收益率也越大，否则，该证券就只会增加证券组合的风险，却不能同比增长预期收益率，这样的市场证券组合也就算不上是最佳的市场风险组合投资。所以，人们只要从中剔除这种不起积极作用的证券，就可使该组合的预期收益率相对于它的风险度而增加。因此，可以说β值与预期收益率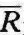是一种正相关关系，也可以说，无风险证券的β值等于零。证券组合相对于自身的β值就是1。(www.xing528.com)

证券与证券组合的β值，衡量的是相对于某一特定证券组合——市场证券组合而言，证券于证券组合收益的波动性。个别公司因经营亏损发生股价剧烈波动的情况不应在β值的衡量范围内。β值衡量的风险是属于系统风险，即无法通过投资分散化予以消除化解，而非系统风险由单个证券的收益波动来决定，可通过投资分散化来消除。人们只须知道某个证券在过去一系列的收益数据，以及作为参照物的特定证券组合，即市场证券组合在相应年份的变动数据，就可得出该证券的β值，而证券组合的β值就是该组合中各证券β值的加权平均数。

根据资本市场线的公式，可以将上述公式变换成：

式中，

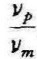表示某个有效证券或有效证券组合风险度在市场证券组合风险度中的比重，也就是上述提到的证券组合波动性与市场波动性的比例，可以用β值表示。这样某个证券的预期收益率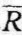i，可用公式表示为：

进一步还可用图6-5展开说明：

图6-5

这条证券市场线表明各种证券的收益率与以β值作为衡量测度风险之间的关系。在证券市场线上，这M点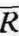（m、1.0）表示某个有效证券或有效证券组合的预期收益率与市场证券组合的预期收益率相符。这个市场证券组合即上述提到的以某个具有一定权威性的股指作为测定的基准。当β值小于1，表示某证券的预期收益率将低于市场预期收益率，或者说，某证券的风险度低于市场风险度。在实际操作中，人们如要计算某有效证券或有效证券组合的预期收益率，那么，应首先获得以下三个数据：无风险利率Rf、市场证券组合预期收益率Rm，以及β值。

假定某证券的无风险利率是3％，市场证券组合预期收益率是8％，β值为1.1，则

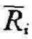＝Rf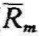＋（－Rf）×β＝3％＋（8％－3％）×1.1＝8.5％

可见，β值可替代方差作为测定风险的指标，它与有效证券或有效证券组合的预期收益率成正相关关系。