马柯威茨的均值方差理论解析

在介绍马柯威茨均值方差理论前，必须先了解证券组合投资的基本概念。证券组合，是投资者对各种证券商品进行一定的选择而形成相对固定的若干个投资品种，以达到在一定的约束下，实现投资收益最大化的基本目标。这种组合并非是若干个证券商品简单随意的拼凑，它应体现出投资者的意愿和所受的约束，是经过精心选择和科学搭配的，并可随时调整，使其不偏离投资者的预定目标，也就是在投资收益与风险的权衡中作出的最佳组合，也是希望达到投资本金安全、投资收入相对稳定并逐步实现资本增值的一个综合目标。

要想达到这近乎完美的目标，人们往往根据证券的基本面分析，采用静止的、历史的资料数据，以自己的感性认识和直觉判断来进行证券商品的投资组合，而较少有一系列较为精确的科学计算方法。因此，所得到的只能是一个定性分析的原则，缺乏定量分析的具体化，在究竟承受多大风险，证券分散到某种程度，在哪一点上才能达到高收益与低风险的最佳组合上缺乏明确具体的判断。正是为了弥补这种不足，证券组合理论才应运而生，哈里·马柯威茨（Harry M.Markowitz）是该理论的创始人和代表人物。证券组合理论的主要内容是在投资者为追求高的投资预期收益，并希望尽可能躲避风险的前提下，阐述了一整套理论框架，并运用二维规划一套复杂的数理统计方法，以解决如何最有效地分散组合证券风险，求得最大收益。其立论是：人们在任何投资预期收益上，宁愿证券组合的风险承受是最小的，而在任何既定的投资风险上，要追求投资预期收益的最大化；或者说，不愿承担无相应期望收益加以弥补的额外风险，以达到证券风险和收益最有效交换的完满境地。均值方差理论奠定了证券组合理论的基本框架，通过风险测量较为准确地计算出投资者收益和成本遭受损失的可能性大小，在此基础上，经过许多学者的不断完善和发展，证券组合理论逐渐形成。

1.证券组合均值或预期值的计算

任何一种证券的投资收益都是不确定的，收益的不确定性存在于一切证券投资之中。人们既要考虑各种投资收益发生的可能性，即其概率分布，又要考虑到各种收益的绝对值。均值就是投资的预期收益，或者称预期值，采用证券投资的各种可能收益的加权平均值，以各种可能收益发生的概率作为权数，证券组合的预期收益率公式表达为：

式中，

为证券组合收益预期收益率；

为证券i的预期收益率；

Xi为投资于证券i的期初市场价值在组合中所占的比重；

n为证券组合数目。

这里，为了理解某证券的预期收益率，再给出某证券i的预期收益率的公式：

式中，

Rij为证券i第j种可能的收益率；

ρ（Rij）为证券i收益的第j种可能性的概率；

n为可能性的总和。

某人投资四只股票，组成一证券组合，经多方分析研究，他认为在不同时期，四只股票有可能获得的收益率以及相对应的每一结果可能发生的概率，可大致依据公式（2）计算得出的各股的预期收益率（见表6-1）。

表6-1 四只不同股票的预期收益率表

如果知道了某一只股全部收益结果出现的概率，那么无论其结果发生的概率是否都相同，投资者的证券组合预期收益率就等于全部收益结果与其发生概率之积相加的总和，即公式（1）。

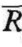ρ＝0.2×18.3％＋0.4×20.5％＋0.3×20.6％＋0.1 ×24％＝20.44％

2.证券组合的方差——确定风险测度指标的计算

方差（或称标准差）是统计学中最基本的测算工具之一。在确定性的条件下，投资收益率即是决策的最好依据，而在不确定性条件下，仅靠上述预期收益率一个指标来判断某证券商品的优劣并为此作出是否投资的决策是远远不够的，甚至是轻率的。人们还必须考虑如不能实现预期收益而要面对的风险。如前所述，投资预期收益并不等于实际收益，实际收益率完全可能高于、低于或等于预期收益率。这种围绕预期收益率波动的程度越大，即上下振幅越大，实际收益率与预期收益率之间的差距也越大。投资者不能实现预期收益率的可能也就越大，投资风险也就越大，这种波动程度实际上已成了判定投资成败的第二个指标，也称为风险指标。运用统计学中的方差（标差）VARIANCE来对实际收益率偏离预期收益率的幅度作出估算，也就是对证券投资风险作出数理统计的测度。以下就是方差公式。

式中，(www.xing528.com)

VARi表示某个证券的方差；

VARp表示证券组合的方式。

这两种比率之间离差的估算，显然无法用各证券的方差加权平均求得证券组合的方差值，因为各证券商品的风险与证券组合的风险数值是不同的。在许多情况下，往往前者要大于后者，道理很简单，证券组合的风险不仅取决于构成它的各单个证券的风险，也取决于这些独立的单个证券商品相互之间的关联程度，其中相互抵消的情况是很普遍的。在实际计算中，为了避免各个证券实际收益与预期收益之间的离差在相加求均值时出现正离差与负离差的相互抵消，人们先对每一离差进行平方，然后再对全部离差的平方求其均值，这一结果称之为平均平方离差，简称均方差。有时也用均方差的正平方根来代替均方差，作为衡量证券风险大小的测度，均方差的正平方根，也称为标准差。

3.证券组合与协方差计算

所谓协方差，是两个证券收益离差乘积的加权平均值，是以离差的概率为权数。上述已经提出，证券组合的风险并不等于组合中各单个证券风险的加权平均，它除了与单个证券风险有关外，还与各个证券之间的协方差有关。协方差与方差不同：方差是两个证券收益离差本身平方的平均值，协方差是两种证券与各自离差之积的平均值，方差在任何情况下，都是正数，协方差值可正可负。

当两种证券同时出现上升的收益效果，即各自的离差（R1j－）1，（R2j－）2分别大于零时，或者呈相反情况，即各自的离差分别小于零时，这两离差之积都是正值。协方差英文为COVARIANCE，用COV表示：COV12＞0，由此可以推论，当两种证券同时呈现出相反的结果，即一种证券好的收益结果和一种证券差的收益结果同时出现时，两离差之积就为负数，表示为COV12＜0。换言之，两种证券收益结果变动方向一致，就是协方差大于零。如果两种证券收益结果变动方向无规律无任何关系，其协方差等于零。协方差是衡量两种证券之间收益互动性的一个测度指标，它对证券组合风险起着直接放大或缩小的功能。在单个证券风险和投资比例确定的前提下，协方差就起到了证券组合风险大小的决定性因素。根据以上方差的理解，可以给出证券组合方差的一般公式：

式中，

Xi，Xj为证券i和证券j在证券组合中的比重，即权数；

COV（Ri，Rj）为证券i和证券j收益率之间的协方差；

代表双重加总，所有有关协方差应相加。

4.证券组合与相关系数的计算

为了计算的简便实用，采用某种比例方式将协方差标准化，即用相关系数来代替协方差。相关系数一般采用AB两证券的协方差作分子，它们以各自标准差的积作分母来表示。其取值范围在负1与正1之间。当相关系数取值大于0小于1时，即两种证券之间存在着一种正相关比例，系数越接近1，两种证券之间的这种正相关性越强，证券组合的风险也越大；反之，越趋于0，正相关性就越弱，或者说，负相关性就越强。当系数取值为负1，表明两个证券之间完全负相关，即两个证券彼此之间风险完全抵消，这也是一种理想的投资组合。由此可见，无论人们投资比例如何，只要证券之间不存在完全正相关的关系，即系数小于正1时，证券组合的风险总是会低于单个证券风险的加权平均值，或者说，证券的组合投资总归可在不减少投资预期收益的前提下产生降低风险的效果。

5.有效边界概念与最佳组合

了解了在证券投资组合中通过预期收益和风险指标均方差COV两个指标来研究分析收益与风险的相互关系，以求得在风险既定的前提下，为追求收益的最大化，或在收益即定的前提下，达到最大限度的规避风险。这就是二维规划的含义。用图6-1表示。

图6-1的横轴表示证券组合的投资风险，纵轴表示为证券组合的预期收益水平，任何一种证券组合，都将在图表中找到相对应的一点，全部证券组合，即构成图中ABCD所形成的阴影部分，代表人们面对的所有投资机会。从中可以看出，越是处于图形上端的点，所对应的预期收益就越大；反之，则越小。而越是位于图形右边的点，所对应的投资风险就越大；反之，则越小。显然，A点代表了风险最小的证券组合，B点代表了预期收益最大的证券组合，除此之外，再也不可能存在其他比A点风险更小的和比B点预期收益更大的证券组合，从平面几何的筑图原理知道：这二维规划的可行性区域只能是在第二象限中，如果以360度为所有点的包容区域。那么，最佳的组合点必定都落在270度～360度弧之间。如A点，它是证券组合中均方差最小的一点，即圆弧中270度此点必然可与纵轴相切，其他任何一点都只会加大风险度。而图中B点，它是证券组合中预期收益最大的一点，即圆弧中360度此点必然可与横轴相切，其他任何一点都只会减少预期收益。在圆内的任何一点，都可引申出一条平行线在圆周上找到与其收益相对应的一点，但风险必然更大，即非有效组合。同理，也可引申出一条垂直线在圆周上找到与其风险相对应的一点，但收益必然更小，也非有效组合。可见，只有落在AB弧线上的证券组合才是全部有效组合，AB弧线也是所有证券有效组合的有效边界，在有效边界以内的任何一点投资都是非有效的。我们曾提到的风险最大厌恶者，即最保守的投资者，可选择A点附近的有效组合，虽然收益值较小，但是COV同样也小。反之，雄心勃勃的人们（AGGRESSIVENESS）则可选择接近B点的有效组合，以搏取最大的收益值，同时承担相对应的高风险。这样的观点还可进一步在图6-2上进行分析。

图6-1 证券或证券组合预期收益与风险的投资机会范围

图6-2

无风险利率表示假定可从银行以确定的利率无限制获得贷款，并用其进行风险投资。图中A、B、C、D和A′、B′、C′、D′都是人们进行投资的无差异曲线，它是在此坐标中给人们带来相对满足程度的证券组合点的轨迹，具有正斜率，并且互不相交。显然，处于上方的曲线要比下方的曲线更优，给人们带来更大的满足感，或者说，人们满足的程度依次递减是A大于B，B大于C，C大于D以及A′大于B′，B′大于C′，C′大于D′，但A、B和A′、B′不存在与之对应的投资机会，只有C、D和C′、D′与有效边界有交点。因此，人们自然选择E和E′点进行投资，这两点的区别在于E点的投资者是较为谨慎的，或者说，其风险厌恶程度较大，而E′点的投资者是属冒险性的。此外，其余有效边界上的点都在E和E′点所在的无差异曲线的下方，自然是要被淘汰的。

以上五点是大致介绍了马柯维茨的均值方差理论，它提供了一个权衡收益与风险的定量分析方法，通过这种方法，找到有效证券组合，并从中选择适合自己投资偏好习惯的最佳组合。