探究《五曹算经》和《五经算术》的优化方法

《五曹算经》[250]和《五经算术》[251]为北周甄鸾撰，唐李淳风注释，二书皆入《算经十书》（图3-6）。

图3-6　1890年刻《五曹算经》及其卷端；《五经算术》及其卷端

一、《五曹算经》

《五曹算经》是一部为地方行政官员编写的应用算术书。唐代史料中多有“《五曹》《孙子》等十部算经”一类说法，表明此书是“算经十书”中较受唐代官方重视的一部算书。作为唐宋官方数学教育的教材，《五曹算经》代有刊刻传抄，受到历朝数学家的重视。与十部算经中其他算书相比，《五曹算经》编排和卷名更显著地表明它服务于相应的社会经济制度。因此书所载算题“解题方法都很浅近，数字计算不须要分数的概念”[252]，被视为“稍为有些落后”[253]，研究者往往认为其研究价值不高，而忽略其实用性的一面。其实，《五曹算经》的出现与当时的社会需求有关。

（一）《五曹算经》的撰写背景

北魏太和九年（485），孝文帝颁布法令实行均田制，这项制度一直延续到唐中叶。均田制的实施，使土地面积的计算工作更加频繁。最初可能只需把大块土地划分成小块授予农民，太和九年令则规定民户所受田地“不得隔越他畔”，即每户所受田地应连成一片。但由于这些田地带有桑田、露田等不同性质，往往又被细分为若干段。经过农民还田和官府再授田，或经过多次后代分割继承前代所分桑田等过程，这些小块土地可能会变得越来越细碎，而每块土地的面积都要被丈量出来，因此不仅开始时计算量大，而且频繁计算会长期存在。还有，由于土地被划分为细碎小块及地貌等原因，容易出现各种形状不规则的田地。为应付均田制带来的划分、丈量田地面积的繁重计算量，需要编辑相应的“速算手册”，提供形状足够多的田地的计算法，以便地方官吏遇到某种形状的田地，就能马上依术计算。此外，南北朝时期，战争频繁，一系列与军事活动有关的，如征兵征粮、守城防务、物资集散、军需分配等计算问题必然出现。而从事这些工作的多是基层官吏及下级军官，也需要相应的“速算手册”，遇到问题对号入座，查找相应的算术进行计算。

从《五曹算经》的内容设置和计算方法来看，它完全能满足以上需要。其中虽然一些算法精度不高，但简单便捷、易于掌握，基本能满足当时频繁计算的需要。

（二）《五曹算经》内容概述

《五曹算经》全书五卷，分田曹、兵曹、集曹、仓曹、金曹，共计67题。

1.第一卷田曹

“生人之本，上用天道，下分地利，故田曹为首。”田曹共19题，主要是田亩面积的计算问题，涉及方田、直田、圭田、腰鼓田、鼓田、弧田、蛇田、墙田、箫田、丘田、箕田、四不等田、覆月田、圆田、牛角形田、环田等16种形状的田地，对其面积的近似计算大体可分为4类。

（1）由半对角线求正方形田的面积。田曹第11题，由正方形田的中心到一个顶点的距离（对角线之半）求其面积。其方法为：先求对角线，再据边长与对角线之比为5：7的近似比率，用比例方法求出正方形的边长，然后自乘。对于这类问题，精确的算法是利用勾股定理，由对角线用开方法求出边长，再由边长自乘，得到面积。但这种精确算法需要开方，比较复杂。

（2）四不等田的面积。土地方位通常用“四至”来描述，如果土地面积较大，对丈量精确度又要求不高，一些形状与矩形相去不太远的田地，就能将其近似地作为矩形来处理，这样方田的计算方法通常就能够满足需求。但现实中肯定还存在大量与矩形相差很远的田地，即四不等田（图3-7）。采用的算法是“两组对边平均值的乘积”：

（3）曲边形田地的面积。精确计算曲边形土地的面积，对于地方官吏来说，不仅有些高深，而且麻烦费事。故《五曹算经》将牛角田（图3-8）、覆月田（图3-9）中的曲边，都按直边对待，而将这两种图形，都近似化为三角形来计算面积。

图3-7　四不等田图

图3-8　牛角田

图3-9　覆月田

（4）六边梯形的面积。六边梯形田地的面积，本可通过分为两个梯形，分别计算其面积，然后求和来解决。但《五曹算经》却采用了另一条思路：如腰鼓田（图3-10）、蛇田（图3-11），先算出三广的平均值，再乘以从：

图3-10　腰鼓田

图3-11　蛇田

上述近似算法的误差较大，南宋杨辉《田亩比类乘除捷法》中虽已修正，但其影响到明清两代的一些算术书中还没有纠正过来。究其原因，这些算法虽然降低了计算精度，却简化了运算步骤，便于大量基层官吏掌握和使用。

2.第二卷兵曹

“既有田畴，必资人功，故以兵曹次之。”兵曹共12题，主要是关于征兵、军粮、布阵等方面的简单四则运算题。例如：

今有丁8958人，凡3丁出1兵、问出兵几何？

今有城周48里，欲令防贼，每3步置一兵，问用兵几何？

今有10000人，大将10人，稗将20人，队将100人，散兵9870人，给绢有差，大将人给3丈，稗将人给2丈，队将人给1.5丈，散兵人给9尺，问计几何？

3.第三卷集曹

“既有人众，必资饮食，故以集曹次之。”集曹共14题，主要是关于物资储备、交换贸易方面的问题。例如：

今有豆849斛，凡豆9斗易麻7斗，问得麻几何？

今有席1领，坐客23人，有客533600人，问席几何？

4.第四卷仓曹

“众既令集，必务储蓄，故以仓曹次之。”仓曹共12题，主要是关于物资的征收、运输和粮仓容积计算方面的问题。例如：

今有仓从一丈三尺，宽六尺，高一丈。中有从牵二枚，方五寸，从一丈三尺。又横牵三枚，方四寸，从六尺。又柱一枚，周三尺，高一丈，问受粟几何？

答曰：四百七十一斛奇一百寸。

依术文计算（计算过程中，取1斛=1620立方寸，π=3）结果如下：

仓库总容积130×60×100=780000（立方寸），

从牵（纵梁）体积2×52×130=2×3250=6500（立方寸），

横牵（横梁）体积3×42×60=3×960=2800（立方寸），

圆柱体积302/12×100=7500（立方寸），

仓库有效（受粟）容积（780000-6500-2800-7500）/1620=471斛100立方寸。

计算结果显示，连仓库中的梁、柱所占容积都作了扣除。可见，算法还是很细微周密的。另外，仓曹中还完整地论述了堆集问题（“委粟于地”）的4种计算方法，即

从而验证了计算堆集方法的民间歌谣：

光堆法三十六，倚壁须分十八停，内角聚会时如九一，外角三九甚分明。(www.xing528.com)

5.第五卷金曹

“仓禀货币，交质变易，故以金曹次之。”金曹共12题，主要是关于财务货币、物品买卖方面的问题。例如：

今有钱238贯573文足，欲为92陌，问得几何？

今有贵丝一两值钱56文，贱丝一两值钱42文，有钱132贯810文，问得几何？

综观《五曹算经》全书，田曹为“生人之本”，兵曹以“戍兵屯田”，再论及物资集散、仓储输运、交质变易。可谓环环相扣，体系严密。这一思想颇与《孙子兵法》所论“地生度，度生量，量生数，数生称，称生胜”相合，加之书中多处涉及依丁征兵、守城防务、军需分配等数学问题，故被认为“是我国军事数学方面最早的比较系统的一些记载，这些合乎逻辑的军事数学知识，在四、五世纪之前的世界古代数学资料中也是少见的”[254]。从而，“在世界军事数学史上也应有其重要地位”[255]。

二、《五经算术》

“五经”，即儒家的五部经典。汉班固《白虎通·五经》曰：“五经何谓？谓《易》《尚书》《诗》《礼》《春秋》也。”北周武帝在思想上崇尚儒家，重用儒者，儒家经典大行其道。甄鸾搜集了《周易》《诗经》《尚书》《周礼》《仪礼》《礼记》《论语》《左传》《汉书》等儒家经典与古注中涉及有关数学、律历之处，给以详尽的解释或解答，撰成《五经算术》。

传本《五经算术》分为上下两卷，由《永乐大典》辑出。书中的题，皆出自儒家经典或古注，现举例介绍。

例1：《论语》“千乘之国”法（开平方术）

子曰：“道千乘之国……”注云：“司马法：六尺为步，步百为亩，亩百为夫，夫三为屋，屋三为井，井十为通，通十为成，成出革车一乘。然则千乘之诗赋，其地千成也。”据此，甄鸾编撰一题：

今有千乘之国，其地千成，计积九十亿步。问为方几何？

答曰：三百一十六里六十八步一十八万九千七百三十七分步之六万二千五百七十六。

术曰：置积步为实，开方除之即得。

甄鸾以开方法计算了“千乘之国”的边长，其开方步骤与《孙子算经》相合。用现代数学知识表述如下：

在《五经算术》中，甄鸾还用圆柱求积之法解释了《礼记》“投壶”；用等比数列方法计算《仪礼》丧服的形制等。

例2：求十九年七闰法（历日推算）

《尚书·尧典》曰：“期有三百有六旬有六日，以闰月定四时成岁。”甄鸾以古四分历法作出解释：

置一年闰十日，以十九年乘之得一百九十日。又以八百二十七分，以十九年乘之得一万五千七百一十三。以日法九百四十除之，得十六日，余六百七十三。以十六加上日，得二百六日。以二十九除之，得七月，余三日。以法九百四十乘之，得二千八百二十。以前分六百七十三加之，得三千四百九十三。以四百九十九命七月分之，适尽。是谓十九年得七闰月，月各二十九日九百四十分日之四百九十九。

甄鸾先以一回归年为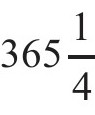日，一朔望月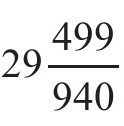日，求出“一岁之闰”为：

由此得出“十九年七闰”：

《春秋·鲁僖公》中有“五年春王正月辛亥朔，日南至”。日南至，即冬至。古代以含冬至之月为“春王正月”。对此句甄鸾给出如下解释：

以积月11985乘周天分27759，得333332691615为朔积分，以日法940除之，得353927为积日，不尽235为小余；以60除积日，取其不尽247为大余，大余定日名，“命以甲子算外”，即正月辛亥朔。

对经书中其他的历日记录，甄鸾均以四分历法推算。

例3：《礼记·月令》黄钟律管法（用“三分损益法”计算十二律）

原文和甄鸾解释文字太多，故不抄录，仅解释其意思。

律，指律调名，或相应的律管。中国古代最早有十二律，据《淮南子·天文训》记载，十二律的名称按音高顺序排列可分为[256]：

黄钟、大吕、太簇、夹钟、姑洗、仲吕、蕤宾、林钟、夷则、南吕、无射、应钟

与今天的音名比较，它们相当于：

C，#C, D，#D, E，F，#F, G，#G, A，#A, B.

按此排列，位于单数者称为“六律”或“阳律”，位于双数者称为“六吕”，或“阴吕”“六同”“六间”。《汉书·律历志》云[257]：“律有十二，阳六为律，阴六为吕。”由此可见，“律吕”就是六律和六吕的合称。

所谓“三分损益法”，就是以三分法来确定各律相对音高或音程关系的数学方法。《史记·律书》记载了这种方法。

生黄钟术曰：以下生者，倍其实，三其法：以上生者，四其实，三其法。

“倍其实，三其法”，即2/3；“四其实，三其法”，即4/3。原文的意思是：“下生者”乘以2/3，实则将原律管（或弦）长分为三份，去其一份，即（1-1/3）=2/3，这称为“损”；“上生者”乘以4/3，实则将原律管（或弦）长分为三份后，加上一份，即（1+1/3）=4/3，这称为“益”。所以，“下生”后的律管（或弦）长比原律管（或弦）短，音增高五度；“上生”后的弦长比原律管（或弦）长，音降低为下方四度。下方四度是上方五度的转位。这样，“上下”交替地推算各律音高或各律管（或弦）长的数值，又称为“上下相生”法。古希腊著名学者毕达哥拉斯（Pythagoras，公元前570至公元前496）所创“五度相生法”，该法只有一个生律因子，即2/3。其计算方法与三分损益法完全相同。

对于十二律的相生顺序，最早的记载见《吕氏春秋·音律》[258]：

黄钟生林钟，林钟生太簇，太簇生南吕，南吕生姑洗，姑洗生应钟，应钟生蕤宾，蕤宾生大吕，大吕生夷则，夷则生夹钟，夹钟生无射，无射生仲吕。三分所生，益之一分以上生；三分所生，去其一分以下生。黄钟，大吕，太簇，夹钟，姑洗，仲吕，蕤宾为上；林钟，夷则，南吕，无射，应钟为下。

《淮南子·天文训》也记述了十二律相生，其相生顺序同《吕氏春秋·音律》，见图3-12。

图3-12　《淮南子·天文训》十二律相生顺序图

甄鸾按照《淮南子·天文训》的方法，取黄钟宫音律管长9寸、律数81（“黄钟之律，九寸而宫音调。因而九九八十一，故黄钟之数立焉……”），用“三分损益法”计算了十二律的律管之长。计算过程中取了整数而略去小数，结果如下：

黄钟律管管长9寸，

甄鸾以同样的方法还计算了京房的六十律。

综观《五经算术》，就数学的内容而论价值有限，但对研究经学的人会有一定的帮助。另外，从数学和文化交互影响的历史观点看，《五经算术》是一部重要的文献。