环节一：聚焦问题
1.导入：大树，随处可见！在森林、在路边，在我们美丽的校园里。（出示四校区树木照片）树不仅能美化环境，还能净化我们的空气。你们知道树是怎么净化空气的吗？
2.核心问题：小小的叶面多么神奇啊。今天我们就来一起研究叶面的大小，也就是树叶的面积。
【设计意图】 从校园中的树木、身边的落叶讲起，小小的树叶是植物进行光合作用的主要场所。小事物、大知识，从而引导学生关注叶面的大小，引发学生的学习兴趣，为后续活动作铺垫。
环节二：初步尝试，说困难，想策略
1.出示活动要求：请你想办法得到树叶的面积，并把你的想法清楚地写在学习单上。
2.学生独立思考，并尝试说出自己遇到的困难以及启发。
预设：可以把树叶拓在纸上，数方格、切割成一些规则图形……
【设计意图】 在求树叶的面积的初次尝试中，学生会无从下手，学生通过独立思考发散思维，寻找解决办法。当遇到困难时，学生可以通过小组合作的学习方式在相互启发中碰撞出思维的火花，进一步思考与探索。
环节三：再次尝试，齐汇报，说利弊
1.在几位同学的启发下，再次尝试。
2.展示学生的解决方法。
预设：
（1）画方格，数单位面积的个数：方格大小不同；
（2）树叶内画最大的长方形；
（3）树叶外画一个长方形；
（4）分成若干个三角形、梯形或长方形；
……
3.小组讨论。
（1）汇报中提到的方法你能看懂吗？能不能表述清楚？
（2）互相说一说这些方法是怎么想到的。
（3）互相讨论这些方法是否可行，可行的方法好在哪，不可行的方法可以怎么改进？
4.全班汇报交流，教师适时追问和总结提升。
（1）数方格法。
追问：方格有大有小，不同之处是什么？哪个准确，为什么？怎样可以更准确？
预设：方格更小的比方格大的准确。因为方格越大，边缘部分格子不完整的就越不准确，变成小格子后有一部分格子完整了，就准确了一些（见图5-11和图5-12）。
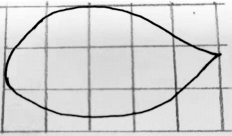(www.xing528.com)
图5-11 大方格
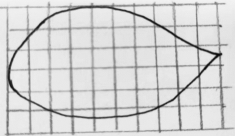
图5-12 小方格
（2）切割法。
追问：为什么要这么切？为什么要切成大大小小的这么多，那么小的地方也不放过？怎样可以更准确？
预设：这样就转化成了规则图形，可以利用面积公式来计算了。切割这么多是为了更准确。边缘部分再继续切割成更小的部分则更准确（见图5-13）。
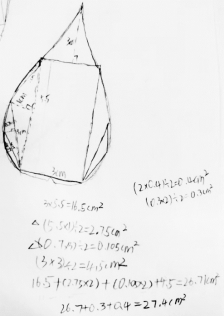
图5-13 切割法
（3）割补求和法。
追问：只剪一个不行吗？怎样缩小误差？
预设：把边缘部分再剪成规则图形可以缩小误差（见图5-14）。
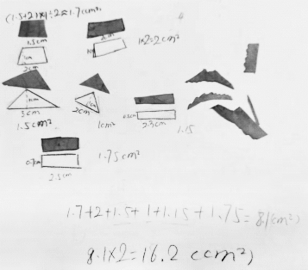
图5-14 割补求和法
（4）逐渐逼近法。
追问：怎样可以更准？
预设：从外部和内部逐渐逼近树叶，把范围缩小，会更准确（见图5-15）。
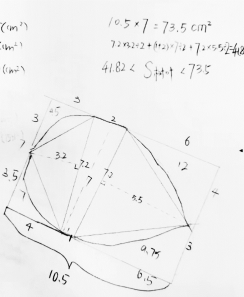
图5-15 逐渐逼近法
（5）你们再想一想，还有没有其他方法？
预设：
a.通过称重的方法想办法得到树叶的面积。把树叶剪成一平方厘米的小方块，比如100块，称出一小块树叶质量。再称出一个树叶的质量，相除即可得到树叶的面积。
b.用铺豆子的方法，用豆子铺满树叶，再把豆子铺成规则的图形求得面积。
追问：用这种方法的误差在哪儿，怎样可以更准确？
预设：豆子之间有缝隙会造成误差。可以用更小的豆子铺，这样豆子间的缝隙会更小，误差也就更小了。
5.仔细观察你们的这些方法，有什么发现或有什么想法？
6.教师小结：遇到不规则图形面积的问题时，我们用已经学过的知识和办法来尝试解决。没有办法得到树叶的真实面积，但通过一些方法来缩小面积的近似值和真实值之间的误差，我们离真实值又进了一步。
【设计意图】 学生在原有经验认知基础上解决新问题，渗透着“转化”思想方法和“极限”思想方法。不同的方法可以让学生感受不同的探究路径，让算法多样化，更利于学生理解算理、探究数学的本质，学生能够感受到实验带来的快乐，增加探究下去的欲望。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
