高中数学导研式教学的优化注意事项

导研式教学在实践中暴露出的问题主要包括两方面：一是导研式教学设计模型和教学模式存在的问题；二是教师对导研式教学设计模型和教学模式理解不到位或使用不当带来的问题。从前面实施的情况，尤其是骨干教师的教学实践来看，有许多事项值得注意。

（一）使用导研式教学设计模型的注意事项

1.应灵活使用，而不是生搬硬套

教学对象、教学内容、教学情境和教学设计主体的复杂性决定了教学设计必须因人、因内容、因情境而异。尽管教学设计模型提供了教学设计的基本框架和技术路线图，但它应与具体实际相结合。例如，在设计教学目标时，其思维导图是从学习习得内容、习得程度、习得方式、习得差异四个方面来设计的，但在具体思考与设计时，也可以从知识与技能、过程与方法的习得内容、习得程度、习得方式、习得差异等方面来进行；也可以按教学事件发生的时间顺序来思考与设计。教学设计模型作为一种概念框架和思维导图，并不是要逐项套用的，而是提供一种指导和辅助工具，即需要的时候用，不需要的时候就不用；能用的时候用，不能用的时候则不用。

2.应加强教学设计的前期分析

教学设计是一项系统工程，应在坚实可靠的基础上进行。传统备课强调，要“吃透两头”（即教材和学生），“把握三点”（即突出重点、突破难点、抓住关键点），这对现在的教学设计仍有十分重要的指导和借鉴价值。当下教学设计需要进一步丰富与拓展“吃透两头”“把握三点”的内涵，并使之精细化、具体化和操作化。

教学设计的前期分析主要包括学习内容分析、学生认知分析和学习环境分析三方面，它类似于建大楼、造大桥前的任务分析与地质勘探，打仗前对敌我双方和环境条件等的分析。它既是教学决策的依据，也是教学设计的基础。离开了扎实的前期分析准备，教学设计只能是“想当然、拍脑袋、拍胸部”的决策，所形成的教学设计方案只能是“建立在沙漠上的豆腐渣工程”。教学设计前期分析可参照图4-4、图4-5和图4-6进行：

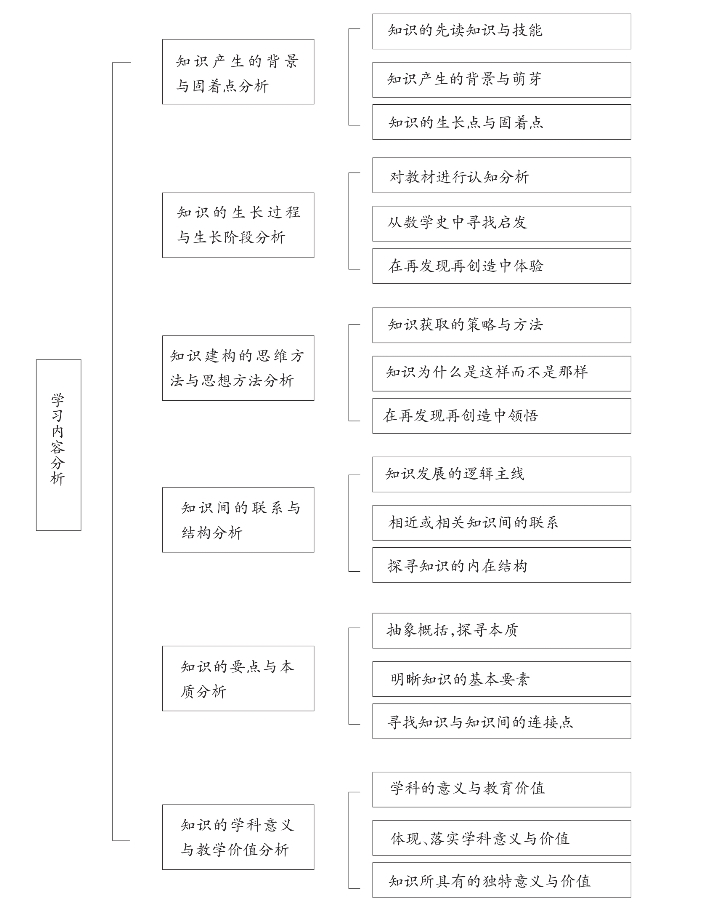
图4-4　学习内容分析思维导图

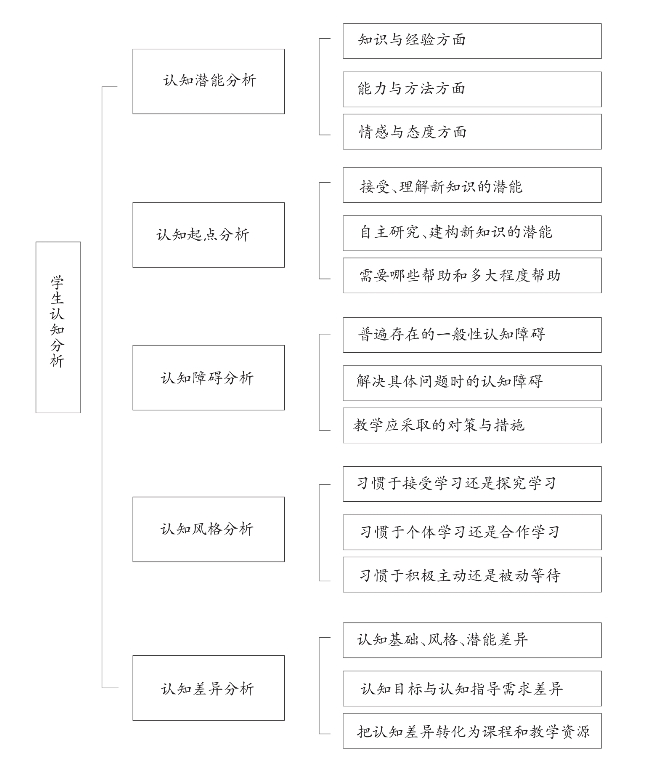
图4-5　学生认知分析思维导图

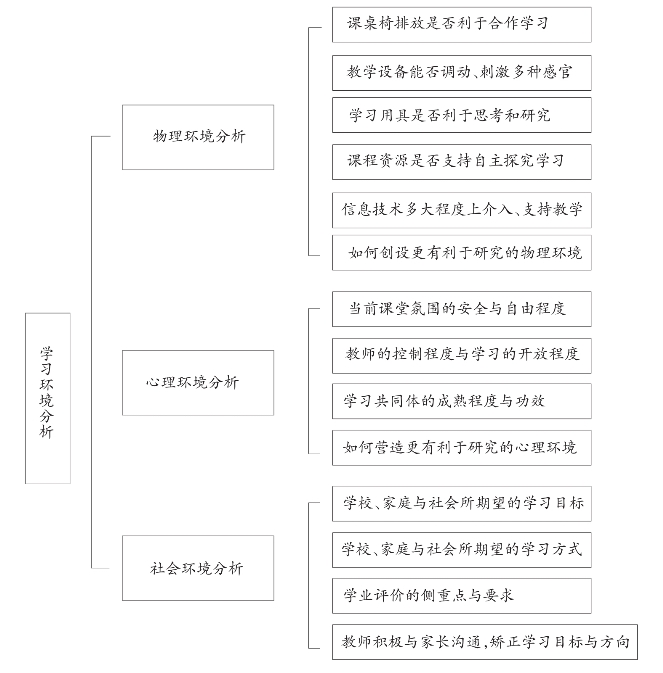
图4-6　学习环境分析思维导图

（二）使用导研式教学模式的注意事项

1.既要“入模”，又要“出模”(https://www.xing528.com)

尽管导研式教学基本模式有比较广的适用范围，但在实际使用时仍需要灵活变通。在“呈现背景，提出问题”环节，有的课在上一节课临近结束时，已经提供了新问题的产生背景，甚至已经提出了新的需要解决的问题，那么就应省略。在“联想激活，寻求方法”环节，如果学生先前没有相关经验，就不存在联想激活的问题，如“弧度与弧度制”的引入就是这样；对于有些内容，如果学生基础扎实、相关知识掌握得好，则可直接寻找解决问题的办法，甚至直接提出猜想、假设，如在学习等比数列时，基础好的学生可以直接进行新知识的发现与建构。在“提出猜想，验证猜想”环节，如果所研究的数学定理、法则是通过逻辑推演直接得到的，而不是通过猜想得出的，那么这个环节也就没有了，或者说是变成了“逻辑推演，得出结论”环节了。“运用新知，巩固内化”环节通常是需要的，但是有时候由于时间的限制，可能安排到下节课；或者第一节课以发现、建构新知识为主，第二节课以巩固与运用所学的新知识为主。在“回顾反思，拓展问题”环节，由于课程标准对学习内容有明确的要求，教材对每个单元，甚至每个课时的知识点都有相对明确的划分，有时提不出有价值又适合学生研究的数学问题，这时最后一个环节就变成了“回顾反思，提炼升华”了。

另外，有的课可能含有两个知识点，要解决两个问题，如前面的“指数函数及其性质”教学就是如此。它既要创设一个具体背景来引出“指数函数”的概念，又要在这个概念得出后再以此为背景研究指数函数的性质。这些课实际上含有两个小的“背景—问题—联想—方法—猜想—验证—巩固—拓展”过程，因此教学应把握导研式教学的精神实质，从学生、教学内容和教师自身的实际出发，灵活变通，而不是生搬硬套，“为模式而模式，为步骤而步骤”。毕竟模式的价值在于需要时“为我所用”，“如何用”，而不是一定要用、一定要照搬。

2.应坚持循序渐进

正如教师在访谈中所指出的：教师变教为导、学生变学为研都不是容易做到的事情，更不是容易做好的事情，教师和学生都需要一个熟悉、适应的过程。实施导研式教学的循序渐进主要有两方面：一方面，教学目标定位应具有适切性、渐进性，即在开始时还是优先落实知识与技能目标，而后不断加大能力教学、思维教学以及培养研究力的力度，避免因教学目标过于“高、大、上”而脱离实际，也避免知识目标与思维目标“两头空”，毕竟只有符合实际的才是最好、最有效的。教师应认识到，把培养与发展学生的研究作为高中数学课程目标是十分恰当的，但作为具体教学目标就不大合适，因为研究力概念比较抽象、理性，操作性不强，在实际教学时应结合具体内容把它细化和实体化，应着力培养学生自主获取知识、建构知识的能力，着力让学生掌握研究某类问题的一般思路和方法，并搞清楚采用这些思路与方法的合理性，甚至必然性。另一方面，教法与学法应具有适切性和渐进性。因为理想的教学设计不一定能够取得理想的教学效果，真正做到有效自主、有效合作、有效探究是很难的，因此教法和学法应与学生的研究意识、研究能力相适应，并随着学生研究力的提高逐步把研究的自主权和核心环节交给学生。

3.不能每节课、每个设计内容都研究

“寸有所长、尺有所短”，没有一种教学模式是完美的，也没有一种教学模式适宜实现所有目标。积极倡导与推广发现法的布鲁纳早就指出：对于学生在数学课上必须掌握的内容，如果全部采用发现法的话，就过于耗时了。我们尚不大清楚如何在发现法与讲授法之间取得最佳平衡，也正在对此进行研究。导研式教学不要求每节课都研究，也不要求什么内容都研究，而是希望抓住核心概念、核心思想方法等教育价值高、迁移功能强的教学内容进行重点研究；导研式教学不排斥其他教学模式，相反，它还积极寻找其他类型教学模式的优点，从而追求教学效益的最大化。

在采取其他教学模式或教学方法时，教师可根据导研式教学理念对其进行恰当的调整与改造，使其更好地与导研式教学融为一体。比如，导研式教学中的预习就不应是传统的学生自学教材，那是接受型的预习，而应是带着问题进行主动思考与探究后再与教材内容进行比较的预习。也就是说，导研式教学中的预习应是一种探索性、研究性的预习。

4.多开展以单元为单位的整体教学

在许多情况下，以课时为单位的导研式教学具有很大的局限性。事实上，导研式教学更适宜于以单元为单位的整体教学和整体设计。例如，在教学正弦定理、余弦定理时，如果以课时为单位，就很容易局限在教材提供的框架内，也就很难提出值得研究的“真问题”，并开展“真研究”；如果硬性地以课时为单位套用导研式教学的模式，就会显得别扭，不符合教学内容的特点；如果以“正弦定理和余弦定理”为单位进行整体设计、整体教学，就能跳出教材对研究内容、研究思路和研究方法的束缚，真正让学生提出“真问题”并进行“真研究”。

又如，指数函数、对数函数和幂函数教学应该作为一个整体进行教学，在指数函数教学中，通过师生共同讨论、反复讨论，建立研究支架，强化对研究某类函数一般思路、策略与方法的教学，从而得出结论；而对数函数和幂函数的教学，则应由学生自主类比指数函数，作为研究函数问题一般思路与方法在实际研究中的运用，学生研究的独立性、自主性应该比指数函数教学更强。

5.不能削弱基础知识与基本技能的学习

尽管理论上知识教学与思维教学应合二为一、相互促进，但在实际教学中由于教师认识和操作不到位等原因，往往做不到，甚至出现知识目标与思维目标都没有落实的情况，因此如何处理知识教学与思维教学的关系是一个重大问题。人无法在真空中思考，数学基础知识与基本技能是数学思维得以进行的前提和基础，把教学的重中之重放在学生思维的培养上是不切实际的。因此，就多数教师的教学而言，一方面，应优先落实思维所赖以进行的基础知识与基本技能；另一方面，应切记“轻而易举地获取了知识，但未必习得了智慧”。在具体教学时，应融知识、能力、思维教学为一体，既要把握好教师呈现问题与学生自主提出问题之间的“度”，也要把握好教师指导与学生自主探究的“度”，以保证学生有足够的时间及时巩固所学知识与技能，防止和避免用不着边际、没有实效的思维教学冲击知识教学。

6.研究不应局限在课内

面对问题与困难，需要借助“循环教学”和“翻转课堂”等理念与做法。所谓“循环教学”，就是在本节课的“回顾反思、拓展问题”环节中提出下节课需要研究的问题，并给予研究方向、研究策略上的指导，然后让学生在课外独立研究，实现研究前移，为下节课教学腾出时间。所谓“翻转课堂”，就是通过微视频、微课、导学案等让学生在课前先对相关问题进行思考与研究，然后再在课堂上讨论、交流，以解决他们难以独立解决的问题。因此，导研式教学应课内与课外通盘考虑来突破课堂教学时间的限制，使学生能够更好地有效研究。

总之，导研式教学设计模型、教学模式的价值在于为教学设计提供一种思维方式和思维框架，而不是要成为“普罗克拉斯蒂铁床”，把活生生的、丰富多彩的教学“削足适履地塞进某一事先设想好的模式之中”。数学教学需要超越一切有序的、规则的和可预测的决定论，走向更为复杂、多元的后现代主义课程观、教学观以及“混浊中的有序与规则”。相应地，教师应在掌握研究型教学基本模式的基础上走向超越模式。