笔者尝试改善高中数学成绩的方式

学生成绩不理想的一个重要原因就是解题时思维障碍，可能由于对数学问题没有整体思路，方法策略不当，知识迁移有误，解题时不能进行有效的调控等。所以，笔者从解除数学成绩不理想解题思维障碍方面进行了一个尝试。

案例

转化对象：笔者在所带的高二班级，根据学生的学习特点选取了其中三名转化对象，为了方便表述，把这三名成绩不理想的学生定名为学生1、2、3，现将这三名成绩不理想的学生的学习特点介绍如下：

学生1：基础差，接受知识慢。对模式化的解题方法接受好，但缺乏创新能力和应变能力，不能举一反三、触类旁通。愿意学习，很刻苦，可惜效果不好，自信心缺乏，有自卑心理。

学生2：高中基础差，人比较聪明，反应很快，学习怕吃苦，没毅力，怕麻烦，解题受阻时往往半途而废。

学生3：数学基础一般，有一定的积累，但是怕吃苦，比较懒惰，不喜欢深究，遇到问题光想走捷径，学习不扎实。

为了使试题有科学性、有效性，符合学生的认识，具有一定的信度和效度，试题是从学生课本的配套练习中选取的。

例：设点P与定点（3，0）的距离和它到定直线的x=12的即离之比是1∶2，求点的轨迹方程。成绩不理想的学生的解法有两种：

方法一：

设点P（x，y），由题意得

两边同时平方得：4（x-3）2+4y2=x2-24x+144

化简整理得：

方法二：

由题意得，（3，0）是椭圆的一个焦点，直线是椭圆的一头条准线。

所以：

得：a2=36，b2=27

所以图椭圆的方程为：

为了对数学成绩不理想进行启发和引导，帮助他们透彻理解概念，掌握基本技能，培养思维品质。笔者对此题进行了变式训练。

变式题：设定点P到定点（2，0），的距离和它到定直线x=3的距离之比为，求点P的轨迹方程。

学生1：设点P的坐标为（x，y），根据题意得：

两边同时平方得：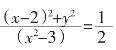

整理得：

学生2：根据题意可得：定点（2，0）是椭圆的焦点，直线x=3是椭圆的一条准线。

∴椭圆的轨迹方程为：

学生3：根据题意可得定点（2，0）是椭圆的焦点，直线x=3是椭圆的一条准线。

得：a2=6，b2=a2-c2=2.

∴P点的轨迹为：

笔者让三位同学聚在一起，让他们一起看看他们的解法。

笔者问同学3：你觉得这两道题是一个类型吗？你用的方法一样吗？

生3：是的。

师：但是为什么第一题对而第二题却错了呢？

笔者问同学2：你解第一题时用了方法一，为什么第二题换了一种方法？

生2：受到了第一题的方法二的影响，感觉第二种方法似乎更简洁。(www.xing528.com)

笔者问同学1：你想过用不同的方法来解这道题吗？

生1：正规方法虽然麻烦一点，不容易出错，很保险，再说也没有时间想多种方法。但是看了他们两个的做法，我也觉得有道理。只是为什么结果不一样呢？

看到他们有点茫然，笔者知道要对他们进行启发，于是笔者提示说：对于第一题的解法一和第二题同学1的解法，你们认为正确吗？

生：正确，这是基本方法。

笔者示意他们说得对，又提示说：对于这两道题，P点的轨迹有什么相同和不同呢？

生：是椭圆。

生1：椭圆的焦点、离心率、准线都不同。

师：还有呢？想想课本上介绍的椭圆都有什么共同特点呢？

生2：它们中心不同。

学生3突然“哦”了一声，笔者感觉他似乎明白了什么，需要给他们时间思考了。几分钟后……

师：问题出现在哪呢？

生3：第一题中，椭圆的中心在原点，所以焦点的横坐标正好是半焦距，但是第二题椭圆的中心不在原点，所以焦点的横坐标不是半焦距。

师：很不错，同学3回答非常正确，而且抓住了问题的关键。

为了进一步提高学生的认识水平，培养他们思维的灵活性，锻炼他们的数学学习意志，笔者紧接着问道：在中心不在原点的情况下，焦半径又是哪段距离呢？

生1：焦点到中心的距离。

师：你们试试能不能不用常规方法做第二题。

【设计意图】

在本题中，学生的错误就是把焦点横坐标一贯性地认为是半焦距。这种错误产生有其合理性。首先，因为在教科书中介绍的椭圆都是中心在坐标原点，椭圆方程都是标准方程，对于焦点在x轴上的椭圆，焦点横坐标的绝对值就是半焦距，中心不在原点的情况没有在学生原有的认识结构中，所以在判断是椭圆之后就习惯性地认为中心在原点。所以，学生2、学生3的解法是符合他们的认识结构的。其次，“学困生”对知识的认识不深刻，只停留在表层，不能抓住问题的实质，按照第一题的固定思维去考虑第二题，形成一种思维定式，造成解题失误。再次，学生在解题过程中容易受以往成功经验的影响，不注意题后反思和归纳总结，缺乏自我监控。比如，成绩不理想的学生3，成功解决例题后不分析例题特点，不对解题过程、解题结果和解题方法进行反思。最后，数学成绩不理想的思维比较单一，比如成绩不理想的学生1，探究问题仅从形式或内容上出发，不善于变化，缺乏多角度思考问题，形成机械模仿的习惯，一旦出现不同的解法就茫然不知所措。基于这些问题，笔者对他们的转化有了方向：

首先，完善成绩不理想的学生的认识结构。在成绩不理想的学生已有的认识基础上，首先给出一种明确的正确解法，然后让学生在此基础上提出自己的解法，发生错误，形成思维冲突，并有意识地适当安排反例，让学生在错误的逆境中前行，通过错误来认识问题实质。最后通过教师的及时点拨，对学生原有的认识结构进行修复和完善。

其次，在平时的教学中，培养学生善于思考、多尝试，不要满足用一种方法得到正确答案；善于对例题进行变化，进行变式教学；多设计一些富有思考意义的练习，通过改变问题的提法，变换条件或结论，变化思考问题的角度培养学生的探究能力；给他们足够的思维空间，引导学生探索问题的本质特征和处理问题的思想方法。

最后，要巧妙地对待学生在解题过程中产生的错误。正视学生的错误，让他们感觉到出错是正常的，善于发现他们在解题过程中微小的闪光点，及时进行鼓励，建立他们的自信和积极向上的进取精神。学生只有在出错后才会自我反省，只有产生冲突才能完善思维。

事实证明，对学生出错的合理运用对成绩不理想的学生是有积极作用的。一天以后，学生1和学生2找到了令笔者惊喜的结果。

解：因为不知道椭圆的中心在坐标原点，但根据题意，中心在x轴上，所以设椭圆的中心坐标为（x，0），

则

a2=（3-x）（2-x）.

又，

所以，即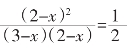

解得x=1，即中心坐标为（1，0），所以c=1，a=，b=1.

所以，P点的轨迹为：

【案例分析】

这一案例给了笔者很大的启迪，比如教师要重视学生的思维过程，要让学生充分暴露思维过程，要善于提出成绩不理想的学生错误解法的合理成分，有针对性地克服学生思维障碍，让学生体验由失败走向成功的快乐和自信。