二次曲线分类的讨论和优化

通过关于化简二次曲线的方程的探讨，可知只要将平面直角坐标系xOy适当地进行坐标轴的平移和旋转，利用坐标变换就能把一般形式的二元二次方程

Ax2＋2Bxy＋Cy2＋2Dx＋2Ey＋F＝0（*）

化为最简二次方程，从而能方便地判定二次曲线的类型，并对曲线的有关性质进行研究．同时还看到，对二次方程（*）进行化简时，如何适当地选择平移和旋转的先后顺序，与方程中的系数B以及系数组δ是否等于0有关．

问题3-3　二次方程（*）中的系数B＝0时，它的曲线Γ可能有哪些情形？

分析　要判断曲线Γ的情形，就要设法将二次方程（*）化为最简二次方程．已知方程（*）中B＝0，如果又有δ≠0，那么可选择平移变换来化简这个方程；如果δ＝0，那么可根据这个方程的特点来选择化简方程的方法．

研讨　二次方程（*）中B＝0，即方程为

Ax2＋Cy2＋2Dx＋2Ey＋F＝0．　

此时，．

（1）如果δ≠0，即AC≠0，那么可通过平移变换对方程化简．

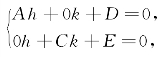解方程组得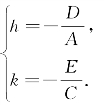

平移平面直角坐标系xOy，将原点移到，则方程简化为

根据方程，对曲线Γ的情形讨论如下：

首先，假设Δ＝0，则方程为Ax′2＋Cy′2＝0．

a．当δ＞0时，AC＜0，方程可变形为

可知它表示两条相交直线，即Γ是两条相交直线；

b．当δ＜0时，AC＞0，方程表示一个点，即Γ是一个点．

其次，假设Δ≠0，则方程可变形为．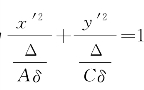

a．当δ＞0时，AC＜0，即A与C异号，因此与异号．这时，方程化为双曲线的标准方程，可知Γ是双曲线．

b．当δ＜0时，AC＞0，即A与C同号，因此与同号．

若与同正，则方程化为椭圆（或圆）的标准方程，可知Γ是椭圆（或圆）；

若与同负，则方程无实数解，可知Γ不存在．

（2）如果δ＝0，此时AC＝0，那么A与C中有且只有一个为0，即方程中仅有一个二次项．根据方程的这个特点，对曲线Γ的情形可进行如下讨论：

首先，假设A＝0，C≠0，则方程呈现为

Cy2＋2Dx＋2Ey＋F＝0．　

还知此时Δ＝－CD2，可得Δ＝0⇔D＝0．

a．当Δ＝0即D＝0时，方程即为

Cy2＋2Ey＋F＝0．　

对于关于y的一元二次方程，判别式Δy＝4E2－4CF．因此，

若Δy≥0即E2－CF≥0，则方程有两个实数解，可知Γ是两条（或重合为一条）平行于x轴的直线

若Δy＜0即E2－CF＜0，则方程无实数解，可知Γ不存在．

b．当Δ≠0即D≠0时，方程可变形为

平移平面直角坐标系xOy，原点移到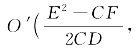，则方程′简化为y′2＝－，可知Γ是一条抛物线．

其次，假设C＝0，A≠0，则方程呈现为

Ax2＋2Dx＋2Ey＋F＝0．

类似于上面对“A＝0，C≠0”的讨论，得到：当Δ＝0且D2－AF≥0时Γ是两条（或重合为一条）平行于y轴的直线，当Δ＝0且D2－AF＜0时Γ不存在；当Δ≠0时Γ是一条抛物线．

对以上（1）（2）讨论中的一些表述，再重新整理如下：

在讨论中，当δ＜0且Δ≠0时，需分析与同正还是同负；当δ＝0且Δ＝0时，需分析D2－AF或E2－CF是否非负．

如果再设方程（*）的一个系数组为H＝A＋C，那么在δ＜0即AC＞0的情况下，可知H，A，C三者同号，则与同正即HΔ＜0；与同负即HΔ＞0．

而在δ＝0且Δ＝0的情况下，出现A＝0且D＝0时需分析E2－CF，出现C＝0且E＝0时需分析D2－AF．而这时E2－CF或D2－AF都可看作是D2＋E2－HF．

于是，对于这个问题研讨所得的结论，可简单归纳如下：

如果二次曲线Γ的方程为，那么

（1）当δ＞0时，若Δ＝0，则Γ是两条相交直线；若Δ≠0，则Γ是双曲线．

（2）当δ＜0时，若Δ＝0，则Γ是一个点；若Δ≠0，则在HΔ＜0的情况下Γ是椭圆（或圆），在HΔ＞0的情况下Γ不存在．

（3）当δ＝0时，若Δ＝0，则在D2＋E2－HF≥0的情况下Γ是两条平行（或重合）直线，在D2＋E2－HF＜0的情况下Γ不存在；若Δ≠0，则Γ是抛物线．

说明　如果方程的曲线Γ是圆锥曲线，那么按照研究本问题的做法，可写出曲线Γ的标准方程，并讨论曲线的有关性质．

在关于方程的曲线情形的讨论中，A＝C≠0是曲线Γ为一个圆的必要条件．另外，当方程中δ＝0且Δ＝0时，若D2＋E2－HF＝0，则Γ是两条重合直线（即一条直线）．

对于二次曲线进行分类时，可以将曲线Γ是一个点或一个圆都列入椭圆的情形，即把一个点看作“点椭圆”，把圆看作“两焦点重合的椭圆”，它们与通常的椭圆一起统称为“椭圆型”曲线．但这样的归并，只是为了便于表述，具体进行分类讨论时还是应将不同情形的椭圆型曲线分辨清楚．

通过对于本问题的研讨可见，二次方程的系数组H，δ，Δ的值是正、是负还是零，是判断方程的曲线情形的基本依据．

用于判断二次方程的曲线情形所依据的条件具有充要性，利用曲线的方程可深入讨论曲线的有关性质．

例9　已知二次方程Ax2＋Cy2＋2Dx＋2Ey＋F＝0的曲线是椭圆，求这个椭圆的长半轴长a、短半轴长b以及半焦距c．

分析　由已知方程的曲线是椭圆，可先写出椭圆的标准方程，再进行求解．

解　对于方程Ax2＋Cy2＋2Dx＋2Ey＋F＝0，它的系数组

由已知方程的曲线是椭圆，可知δ＜0，Δ≠0，且＞0，＞0．此时，A与C同号，与A同号．

通过适当的平移变换，已知方程可化简为椭圆的标准方程

所以，若0＜A＜C或0＞A＞C，则＞，这时

若A＞C＞0或A＜C＜0，则＜，这时

说明　利用椭圆的标准方程，可以直接求出椭圆的长半轴长a、短半轴长b和半焦距c．注意，它们保持关系式a＞b＞0和a2＝b2＋c2．

一般而言，几何量a，b，c是描述椭圆几何特征的数量，其大小应由给定的椭圆所确定，即a，b，c的值不会因这个椭圆的方程表达式发生变化而改变．

针对这个椭圆有关几何量的大小与椭圆的方程表达式无关，初步讨论如下：

在本题中，若将坐标原点移到O″（h′，k′），通过平移变换后已知方程变为方程

Ax″2＋Cy″2＋2D″x″＋2E″y″＋F″＝0，　′

则方程′与已知方程表示同一椭圆．在方程′中，D″＝Ah′＋D，E″＝Ck′＋E，F″＝Ah′2＋Ck′2＋2Dh′＋2Ek′＋F；系数组是．

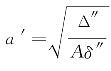这时，不妨设0＜A＜C，则如同解答本题一样，可导出方程′所表示的椭圆其长半轴长，短半轴长．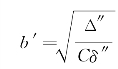

因为δ″＝δ＝－AC，而且

所以，可得a′＝a，b′＝b，c′＝c．

在上述讨论中可见，δ″＝δ和Δ″＝Δ是这类平移变换前后两个方程的系数组之间的固有关系，这种关系与“曲线有关几何量的大小是确定的”具有一致性．

问题3-4　二次方程（*）中的系数B≠0时，它的曲线Γ可能有哪些情形？

分析　可按照问题3-2的做法，通过旋转变换将二次方程（*）简化为不含两“元”乘积项的新方程；然后，再如同对待问题3-3那样进行研究．

研讨　已知二次方程（*），其中B≠0．

取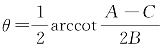，将平面直角坐标系xOy的坐标轴旋转θ角，得到曲线Γ关于坐标系x′Oy′的方程为方程．方程与方程的形式一样，因此可类似于问题3-3的研讨那样，对方程的曲线情形进行讨论．

将方程的三个系数组分别记作H′，δ′，Δ′，在归纳对方程的曲线情形讨论所得的结论时，可参照问题3-3所得的结论．由于方程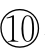与方程（*）表示同一曲线，因此可将H′，δ′，Δ′的值是正、是负还是零作为基本依据，对方程的曲线即曲线Γ的情形进行判定．

说明　对本问题研究所得的结论进行表述时，可直接以方程的三个系数组H′，δ′，Δ′的值是正、是负还是零为基本依据．由此可知，只要通过旋转变换将二次方程（*）化为方程，就能对曲线Γ的情形进行判定．

如果由方程判定了曲线Γ是圆锥曲线，但还要指出它的标准方程，那么就要将方程进一步化为最简二次方程．这时，可参照问题3-3的具体做法，再将坐标系x′Oy′适当进行平移，使得曲线Γ关于新坐标系x″O′y″的方程是最简二次方程；然后写出曲线Γ关于坐标系x″O′y″的标准方程（求标准方程的一般过程参见第3．2节例8）．

对于问题3-4研究所得的结论，如果要求直接用方程（*）的系数组H，δ，Δ的数值特征来表述，那么就要进一步考察在研究过程中涉及的H′与H，δ′与δ，Δ′与Δ这三对系数组数值之间有何关系．联想例9中通过探求一个椭圆的有关几何量所引出的“特定平移变换的前后两个方程相关系数组之间对应相等”的结论，对于旋转变换前后两个方程的三对系数组之间的关系，则需要考察它们之间是否也有对应相等的关系．

问题3-5　已知二次方程（*）中的系数B≠0，如果利用旋转变换将方程（*）化简为方程

A′x′2＋C′y′2＋2D′x′＋2E′y′＋F＝0，　

那么方程的系数组H′，δ′，Δ′的值与方程（*）的系数组H，δ，Δ的值之间是否有对应相等的关系？(www.xing528.com)

分析　可从二次方程与方程（*）的系数之间的关系着手进行探究．

研讨　取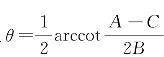，则将坐标系xOy的坐标轴旋转θ角后，二次方程（*）化简为方程．

对于方程，由第3．2节问题3-2对有关系数的讨论可知：

D′＝Dcosθ＋Esinθ，E′＝Ecosθ－Dsinθ．

（1）分析H′与H，δ与δ′

在方程（*）的系数组中，H＝A＋C，δ＝B2－AC．

方程的系数组

（2）分析Δ′与Δ

方程（*）的系数组

方程的系数组

比较Δ′与Δ的表达式，可见只要考察－C′D′2－A′E′2与2BDE－CD2－AE2是否相等．

于是，得

综合（1）（2）可知，方程的系数组H′，δ′，Δ′与方程（*）的系数组H，δ，Δ之间有对应相等的关系，即H′＝H，δ′＝δ，Δ′＝Δ．

说明　研讨旋转变换前后两个方程的系数组的值是否对应相等，关键是要抓住变换前后两个方程的系数之间的关系．在推导Δ′＝Δ的过程中，涉及的代数运算较繁，这时要有耐心，还要善用一些技巧，比如引入t和s，可使运算过程的表述简洁一些．

问题3-6　如果二次方程（*）中的系数B≠0，还有系数组δ＝0且Δ＝0，那么，若利用旋转变换将方程（*）化简为方程A′x′2＋C′y′2＋2D′x′＋2E′y′＋F＝0，则方程的系数组δ′＝0且Δ′＝0，方程成为形如C′y′2＋2E′y′＋F＝0或A′x′2＋2D′x′＋F＝0这样的最简二次方程．这时，用于讨论此方程的曲线情形的判别式是E′2－C′F或D′2－A′F，怎样用方程（*）的系数来表示？

分析　依然从二次方程（*）与方程的系数之间的关系着手进行探究．

研讨　经过以旋转角为的旋转变换后，

（1）如果方程（*）化简得到方程C′y′2＋2E′y′＋F＝0，那么

由于这时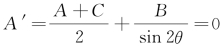，得

又由，得

于是，

由已知δ＝0且Δ＝0，得

（2）如果方程（*）化简得到方程A′x′2＋2D′x′＋F＝0，那么

这时，同（1）一样可推出D′2－A′F＝D2＋E2－HF．

通过以上讨论可知，对于这类特殊的二次方程（*），讨论其曲线情形的判别式可表示为D2＋E2－HF．

说明　通过对问题3-5的研讨，得到H′＝H，δ′＝δ，Δ′＝Δ；再通过本问题的研讨，可知当δ′＝0且Δ′＝0时，判别式E′2－C′F或D′2－A′F的值与D2＋E2－HF的值相等．因此，在问题3-4中对方程的曲线情形进行讨论所得的结论，可类似于问题3-3所归纳的结论那样表述．

一般而言，对于任何一个二次方程的曲线情形进行判断，总可以归结为问题3-3或问题3-4的研讨．还可以看到，二次方程（*）的曲线Γ的情形多样，具体可利用问题3-3和问题3-4所得的结论来判定．其判定过程是：先对平面直角坐标系xOy适当地进行平移和旋转，利用坐标变换将方程（*）化为最简二次方程；然后对曲线Γ的情形作出判断．

下面，将问题3-3，3-4，3-5，3-6所得的结论进行归纳整理．

由二次方程Ax2＋2Bxy＋Cy2＋2Dx＋2Ey＋F＝0的系数，可分别确定三个系数组的值：

通常将H，δ，Δ称为二次方程的曲线Γ的三个基本量，曲线Γ的情形与这三个基本量的正负性（指它们的值是正、是负、还是零）相关．

关于二次方程（*）的曲线Γ的情形，如表1所示．

表1

（续表）

由表1可以看到：

（1）二次方程（*）的曲线可能存在也可能不存在．如果曲线存在，那么它一定是圆锥曲线或退化的圆锥曲线．

（2）二次方程（*）的系数组δ＝B2－AC，其值δ＜0，δ＞0或δ＝0分别是方程（*）的曲线为椭圆（或圆）、双曲线或抛物线的必要条件．

（3）二次方程（*）的系数组Δ＝0是方程（*）的曲线为退化的圆锥曲线的必要条件．

据此对二次方程（*）的曲线Γ进行分类，如表2所示．

表2

（续表）

二次曲线包括圆锥曲线和退化的圆锥曲线．对二次方程（*）的曲线情形进行判定时，首先要分析方程（*）的三个系数组H，δ，Δ的值．这三个基本量的正负性，是曲线分类的基本依据．

例10　判断下列二次方程的曲线的情形：

（1）x2－3xy＋4y2－x－5y＋3＝0；

（2）9x2－6xy＋y2－4＝0；

（3）3x2－2xy＋y2－5x－2y＋30＝0；

（4）ax2－xy＋b＝0，其中a≠0．

分析　从判断δ，Δ，H这三个基本量的正负性着手．

解　（1）对于方程x2－3xy＋4y2－x－5y＋3＝0，

又由H＝1＋4＝5＞0，可知HΔ＜0．

所以，这个方程的曲线是椭圆．

（2）对于方程9x2－6xy＋y2－4＝0，

因为D2＋E2－（A＋C）F＝－10×（－4）＝40＞0，

所以，这个方程的曲线是两条平行直线．

（3）对于方程3x2－2xy＋y2－5x－2y＋30＝0，

又由H＝3＋1＝4＞0，可知HΔ＞0．

所以，这个方程的曲线不存在．

（4）对于方程ax2－xy＋b＝0（其中a≠0），

所以，当b＝0时，Δ＝0，则这个方程的曲线是两条相交直线；当b≠0时，Δ≠0，则这个方程的曲线是双曲线．

说明　一般来说，判断二次方程的曲线情形时，只涉及δ，Δ，H这三个基本量的正负性．因此，通常可以不求出δ，Δ，H的具体数值，只要正确地判定其正负性就可对二次方程的曲线情形作出判断．

在本题（2）中，方程9x2－6xy＋y2－4＝0可变形为（3x－y＋2）（3x－y－2）＝0，可见这个方程的曲线是两条平行直线，即直线3x－y＋2＝0和直线3x－y－2＝0．

在本题（4）中，当b＝0时，这个方程表示直线x＝0和直线y＝ax．一般地，关于x，y的方程ax2－xy＋b＝0（其中ab≠0）可变形为，可知函数（ab≠0）的图像是双曲线．

例11　当实数b满足什么条件时，方程2x2＋bxy＋4y2－6x＋4y－8＝0的曲线是：

（1）双曲线；　　　　　（2）退化的圆锥曲线．

分析　先从二次方程的曲线是双曲线或退化的圆锥曲线的必要条件考虑，再确认其充分性．

解　对于方程2x2＋bxy＋4y2－6x＋4y－8＝0，

（1）这个方程的曲线是双曲线，应满足条件：δ＞0，Δ≠0．

由δ＞0，即－8＞0，得b＜－或b＞；

由Δ≠0，即2b2－6b－108≠0，得b≠9且b≠－6．

所以，当b＜－且b≠－6，或b＞且b≠9时，方程的曲线是双曲线．

（2）这个方程的曲线是退化的圆锥曲线，应满足的条件是：

①δ≠0，Δ＝0；或②δ＝0，Δ＝0，D2＋E2－（A＋C）F≥0．

由①δ≠0，Δ＝0，得b＝9或b＝－6．

由②，因为δ＝0与Δ＝0不可能同时成立，所以满足条件②的b不存在．

所以，当b＝9或b＝－6时，方程的曲线是退化的圆锥曲线．

说明　在表1中列出了判断二次方程的曲线情形所依据的条件，其中针对每一情形的相关条件都具有充要性．