化二次曲线方程为最简形式的方法

我们知道，对于二次曲线Γ关于平面直角坐标系xOy的方程

Ax2＋2Bxy＋Cy2＋2Dx＋2Ey＋F＝0，（*）

可利用坐标轴的平移将它化简．如何通过坐标变换将这个方程化为最简二次方程呢？这是我们要进一步讨论的课题．

为此，先研究下面的问题：

问题3-2　怎样利用坐标轴的旋转来化简二次方程（*）？

分析　经过旋转变换，二次方程中的二次项和一次项的系数都可能发生变化，只有常数项不变．由于指明最简二次方程的表达式中应不含两“元”乘积项，因此可考虑通过旋转变换化去方程中的两“元”乘积项．

研讨　已知平面直角坐标系xOy和二次曲线Γ的方程（*）．

旋转平面直角坐标系xOy，设旋转角为θ，则曲线Γ关于新坐标系x′Oy′的方程为

A′x′2＋2B′x′y′＋C′y′2＋2D′x′＋2E′y′＋F＝0．⑨

其中，常数项与方程（*）中的常数项相同，而系数A′，B′，C′，D′，E′都与θ的取值有关．

由此可见，适当选取旋转角θ，总可化去方程（*）中除常数项外的某一项．

如果方程（*）中B≠0，即含xy项，那么为将方程（*）化为最简二次方程，应考虑利用旋转变换来化去方程中的两“元”乘积项，也就是要适当地选取θ的值，使方程⑨中B′＝0．

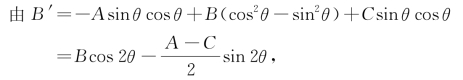
令B′＝0，得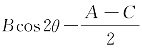sin2θ＝0，即．

可知，取，即取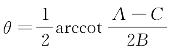时，将坐标轴旋转θ角后，则方程⑨中B′＝0．这时，曲线Γ关于坐标系x′Oy′的方程为

A′x′2＋C′y′2＋2D′x′＋2E′y′＋F＝0．　⑩

其中，系数A′，C′，D′，E′可依据第3．1节例4的结论确定．

如此利用坐标轴的旋转，可将二次方程（*）化简为方程⑩．

说明　对于第3．1节例4结论中关于系数A′，C′的表达式，还可如下进行简化：

由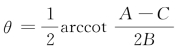，可知，得0＜2θ＜π．

于是，，．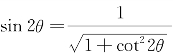

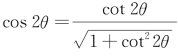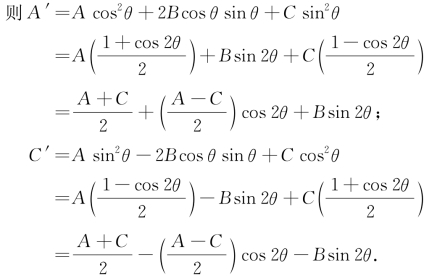
再利用θ的取值能使B′＝0，对A′，C′的表达式作进一步分析：

由B′＝0，即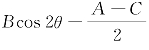sin2θ＝0，得

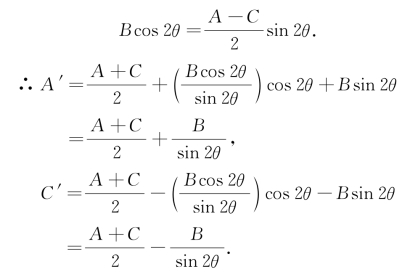
通过对于本问题的研讨可知，只要适当地选取旋转角θ，就可利用旋转变换来化简二次曲线Γ的方程（*）．一般地，取定坐标轴旋转的旋转角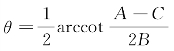以后，就可求出方程⑩中的A′，C′；再由

D′＝Dcosθ＋Esinθ，E′＝Ecosθ－Dsinθ，

利用公式，，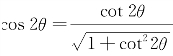

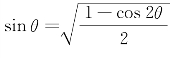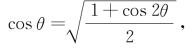
可求出方程⑩中的D′和E′．这样，就可写出方程⑩．

当然，也可在取定旋转角θ后，直接写出旋转公式将它代入方程（*）再进行整理，就得到方程⑩．

在问题3-1和问题3-2的研讨中可见，对二次方程（*）进行化简时，为使过程简便些，就要适当安排坐标轴平移和旋转的先后顺序．选择先“移”还是先“转”，通常如下确定：如果方程（*）中含有一次项且系数组δ≠0，那么先平移；如果方程（*）中B≠0且系数组δ＝0，或者B≠0且不含一次项，那么先旋转．对于方程（*）出现B＝0且系数组δ＝0的情况时，如何确定化简的顺序需要具体分析．

例7　利用坐标轴的旋转，化简二次曲线Γ的方程

x2＋4xy＋y2－16＝0．

分析　曲线Γ的方程中含xy项但不含一次项，可通过先旋转来化简方程．

解　在曲线Γ关于平面直角坐标系xOy的方程中，A＝1，B＝2，C＝1，D＝E＝0，F＝－16．

取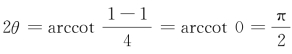，即，得sin2θ＝1．则

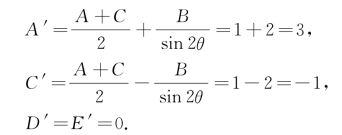(www.xing528.com)

所以，将坐标轴旋转，得曲线Γ关于坐标系x′Oy′的方程为

3x′2－y′2－16＝0．

说明　对于形如Ax2＋2Bxy＋Cy2＋F＝0（其中B≠0）的二次方程，可利用旋转变换来进行化简，所得的新方程A′x′2＋C′y′2＋F＝0是最简二次方程．

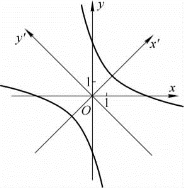
图3-6

对本题中原方程化简所得的方程3x′2－y′2－16＝0再变形，得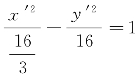．这个关于坐标系x′Oy′的方程是双曲线的标准方程，可知曲线Γ是实轴长为、虚轴长为8的双曲线，如图3-6所示．

对于前面的例6，得到曲线Γ关于坐标系x′O′y′的方程为2x′2－8x′y′＋3y′2－37＝0后，可类似本题再将所得的方程化简，过程如下：

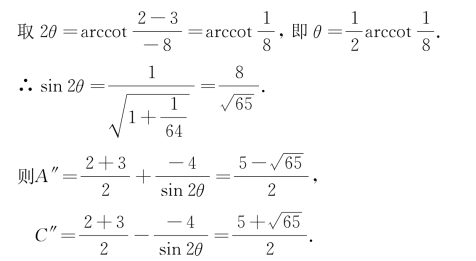
以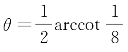为旋转角将坐标轴旋转，得曲线Γ关于坐标系x″O′y″的方程为

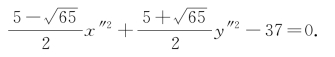
此新方程可变形为

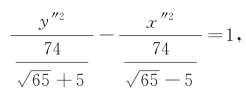
它是双曲线的标准方程，可知曲线Γ是焦点在y″轴上的双曲线．

例8　化简曲线Γ的方程x2＋2xy＋y2＋3x＋y＋4＝0，再进一步分析Γ是什么曲线．

分析　曲线Γ的方程中含有xy项以及关于x，y的一次项．由于δ＝12－1×1＝0，所以不宜从平移着手来化简方程．于是考虑先通过旋转变换化去方程中的xy项，然后再分析能否进一步简化，从而对Γ是什么曲线作出判断．

解　在曲线Γ关于平面直角坐标系xOy的方程中，A＝B＝C＝1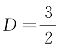，，，F＝4．

取，即，得sin2θ＝1．则

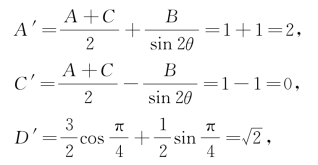
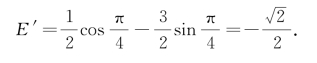
所以，将坐标轴旋转，得曲线Γ关于坐标系x′Oy′的方程为

上面这个方程中含有关于x′的二次项和一次项，于是按x′配方并变形，得

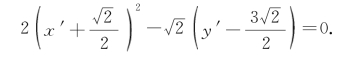
令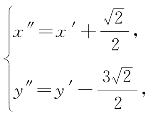即平移坐标系x′Oy′，将原点移到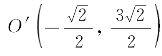，则曲线Γ关于坐标系x″O′y″的方程为

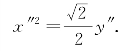
这个方程是抛物线的标准方程，可知曲线Γ是焦距为的抛物线．

说明　在本题解答中，通过坐标变换化简了二次方程的表达式，所得到的新方程是抛物线的标准方程，从而可以判定曲线Γ是抛物线．

利用旋转变换来化简本题中曲线Γ的方程时，也可直接运用旋转公式来确定新方程．基本过程是：

取，将坐标轴旋转，得旋转公式为

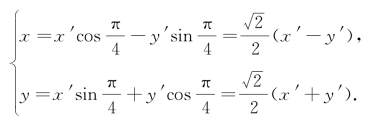
代入原方程，整理得．

由本题解答中最后所得的抛物线Γ的标准方程可知，坐标系x″O′y″的原点O′是抛物线Γ的顶点．如果还要进一步指出抛物线Γ的顶点在原坐标系xOy中的坐标，那么可运用坐标变换公式分步求出．过程如下：

在坐标系x′Oy′中，O′的坐标为；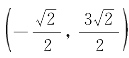

在坐标系xOy中，O′的坐标分量分别为

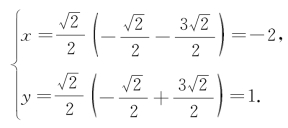
图3-7

所以，抛物线Γ的顶点O′在原坐标系xOy中的坐标是（－2，1）．抛物线Γ如图3-7所示．