利用平移简化二次方程

已知二次曲线Γ关于平面直角坐标系xOy的方程为

Ax2＋2Bxy＋Cy2＋2Dx＋2Ey＋F＝0．（*）

问题3-1　怎样利用坐标轴的平移来化简二次方程（*）？

分析　经过平移变换，二次方程中的二次项系数不会发生变化，而一次项系数及常数项随之改变．因此，可考虑通过平移来化去方程（*）中的一次项．

研讨　已知平面直角坐标系xOy和二次曲线Γ的方程（*）．

平移平面直角坐标系xOy，将原点移到O′（h，k），则Γ关于新坐标系x′O′y′的方程为

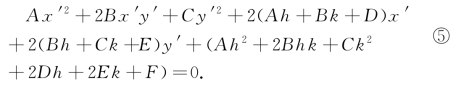
如果h，k能使Ah＋Bk＋D＝0且Bh＋Ck＋E＝0，那么方程⑤中就不含关于x′，y′的一次项．也就是说，如果关于h，k的一次方程组

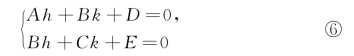
有解，那么就可通过平移变换将方程（*）化为不含一次项的方程．

关于h，k的方程组⑥的系数行列式是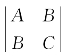，行列式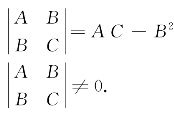．方程组⑥有唯一解的充要条件是

通常，设方程（*）的系数组δ＝B2－AC，则

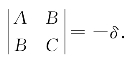
由以上讨论可知，如果δ≠0，那么方程组⑥有唯一解（h，k），且得

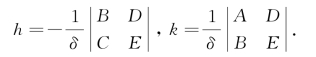
这时，平移坐标系xOy，将原点移到O′（h，k），则方程（*）化为

Ax′2＋2Bx′y′＋Cy′2＋F′＝0．　⑦

其中，常数项F′＝Ah2＋2Bhk＋Ck2＋2Dh＋2Ek＋F．将F′的表达式变形，得

F′＝（Ah＋Bk＋D）h＋（Bh＋Ck＋E）k＋（Dh＋Ek＋F）＝Dh＋Ek＋F．

再将由方程组⑥解得的h，k的值代入上式，得

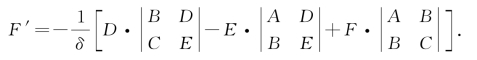
设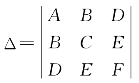为方程（*）的另一个系数组，可知

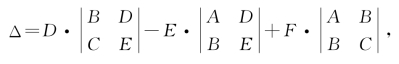
则．

于是，曲线Γ关于坐标系x′O′y′的方程为

说明　对于满足条件δ＝B2－AC≠0的二次方程（*），可通过适当的平移变换化去方程中的一次项，由此得到曲线Γ关于新坐标系x′O′y′的方程为方程⑧．

可利用方程⑧，进一步分析曲线Γ的几何特征如下：

在方程⑧中，如果同时用－x′代替x′，－y′代替y′，那么这个方程的表达式保持不变．这就是说，曲线Γ关于坐标系x′O′y′的原点O′对称，即点O′（h，k）是曲线Γ的对称中心．

一般来说，如果方程（*）的系数组δ＝B2－AC≠0，那么二次曲线Γ有一个对称中心，并称Γ为有心二次曲线．这时，可由方程组⑥求出二次曲线Γ的对称中心．设这个对称中心为O′（h，k），则平移坐标系，将原点移到O′，可使方程（*）化为方程⑧的形式．

如果方程（*）的系数组δ＝0，那么关于h，k的方程组⑥有无数个解或者无解，这时一般不宜从平移着手对方程（*）进行化简．

例5　利用坐标轴的平移，化简二次曲线Γ的方程

4x2＋9y2－8x＋18y－23＝0．

分析　由曲线Γ的方程，得δ＝02－4×9＝－36≠0，因此可求出Γ的对称中心，再通过平移变换化去方程中的一次项．如果注意到这个方程中不含xy项，那么也可对这个方程分别按x，y配方，然后直接进行变量代换来化简方程．(www.xing528.com)

解法一　在曲线Γ关于平面直角坐标系xOy的方程中，A＝4，B＝0，C＝9，D＝－4，E＝9，F＝－23．系数组δ＝02－4×9≠0．

作关于h，k的方程组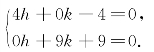

解方程组，得h＝1，k＝－1．

这时，F′＝－4×1＋9×（－1）－23＝－36．

所以，平移坐标系xOy，将原点移到点O′（1，－1），则曲线Γ关于坐标系x′O′y′的方程为

4x′2＋9y′2－36＝0．

解法二　将曲线Γ关于平面直角坐标系xOy的方程分别按x，y配方，得

4（x2－2x＋1）＋9（y2＋2y＋1）－4－9－23＝0，

即　4（x－1）2＋9（y＋1）2－36＝0．

令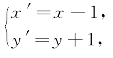　代入上面这个方程，得

4x′2＋9y′2－36＝0．

所以，曲线Γ的方程可化为

4x′2＋9y′2－36＝0．

说明　本题解法一，是对于满足条件δ≠0的二次方程，利用平移变换化去所含一次项的通用方法．

而由解法二可见，对于形如

Ax2＋Cy2＋2Dx＋2Ey＋F＝0（其中AC≠0）

的二次方程（即不含两“元”乘积项的二次方程），可先将这个方程分别按x，y配方，再进行变量代换（其实就是相对于直角坐标系进行平移变换），这样也可化去方程中的一次项．

通过平移变换将二次方程Ax2＋Cy2＋2Dx＋2Ey＋F＝0化简，所得的新方程是表达式为Ax′2＋Cy′2＋F′＝0的最简二次方程．

对本题中原方程化简所得的方程4x′2＋9y′2－36＝0再进行变形，得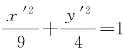．这个关于坐标系x′O′y′的方程是椭圆的标准方程，可知曲线Γ是长轴长为6、短轴长为4的椭圆．

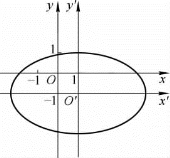
图3-5

椭圆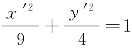如图3-5所示．

例6　利用坐标轴的平移，化简二次曲线Γ的方程

2x2－8xy＋3y2－16x＋22y－10＝0．

分析　在曲线Γ的方程中，δ＝（－4）2－2×3＝10≠0，因此可求出曲线Γ的对称中心，再通过平移变换化去方程中的一次项．

解　在曲线Γ关于平面直角坐标系xOy的方程中，A＝2，B＝－4，C＝3，D＝－8，E＝11，F＝－10．系数组δ＝（－4）2－2×3≠0．

作关于h，k的方程组

解方程组，得h＝2，k＝－1．

这时，F′＝－8×2＋11×（－1）－10＝－37．

所以，平移坐标轴，将原点移到点O′（2，－1），则曲线Γ关于坐标系x′O′y′的方程为

2x′2－8x′y′＋3y′2－37＝0．

说明　对于含有xy项的二次方程，经过平移变换后所得的新方程中一定含有x′y′项且此项与xy项同系数．如果含xy项的二次方程满足条件δ≠0，那么可通过平移变换来化去方程中的一次项，但这时一般不考虑用“配方”法来化简．

本题中曲线Γ关于坐标系x′O′y′的方程中含有x′y′项，可考虑再通过旋转变换来进一步化简这个方程．