坐标轴的旋转及其特点

对于一个平面直角坐标系，不改变原点的位置和坐标轴的单位长度，只是将两坐标轴按同一方向绕着原点旋转同一角度，这样的变换叫做坐标轴的旋转，简称旋转．

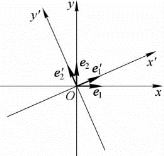
图3-3

如图3-3所示，平面直角坐标系xOy的两坐标轴绕着原点O旋转θ角后，得到新坐标系x′Oy′；规定逆时针旋转θ为正，顺时针旋转θ为负；单位向量e1，e2以及e′1，e′2的方向分别与x轴、y轴、x′轴、y′轴的正向相同．

在坐标系xOy中，

e′1＝（cosθ，sinθ），

设点P在平面直角坐标系xOy和x′Oy′中的坐标分别为（x，y）和（x′，y′），则

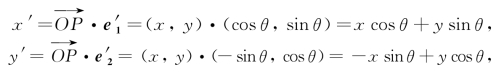
即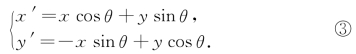

相对而言，也可将坐标系xOy看作是由坐标系x′Oy′按（－θ）角进行旋转后得到的新坐标系，这时，

即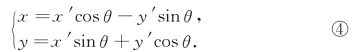

式③和④是关于坐标轴旋转的坐标变换公式，简称旋转公式．

利用公式③，可从点的旧坐标（x，y）求得它的新坐标（x′，y′）；利用公式④，则可从点的新坐标（x′，y′）求得它的旧坐标（x，y）．

例3　将平面直角坐标系xOy的坐标轴旋转，得到新坐标系x′Oy′，求：

（1）点A（2，－3）和B（－1，4）的新坐标；

（2）直线l：x－＋2＝0和曲线Γ：x2－＋2y2－12＝0关于新坐标系的方程．

分析　直接利用旋转公式进行变换．

解　（1）由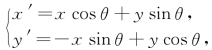其中，得

所以，点A（2，－3）的新坐标是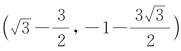；点B（－1，4）的新坐标是．

（2）由其中，得

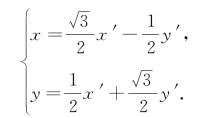
将这个旋转公式代入直线l的方程，得

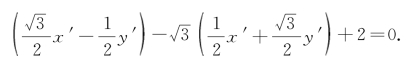
化简后，得y′＝1．

再将这个旋转公式代入曲线Γ的方程，得(www.xing528.com)

展开后整理，得x′2＋5y′2－24＝0．

所以，直线l关于坐标系x′Oy′的方程是

y′＝1；

曲线Γ关于坐标系x′Oy′的方程是

x′2＋5y′2－24＝0．

说明　已知一个点在旧坐标系中的坐标，可直接利用旋转公式③来求出这个点的新坐标；而已知一条曲线关于旧坐标系的方程，则通常利用旋转公式④，通过代换来求这条曲线关于新坐标系的方程．

通过旋转变换，得到曲线Γ关于坐标系x′Oy′的方程是x′2＋5y′2－24＝0，即．这个新方程是椭圆的标准方程，可知曲线Γ是长轴为、短轴为的椭圆．

图3-4

直线l和椭圆Γ如图3-4所示．

例4　已知二次曲线Γ关于平面直角坐标系xOy的方程为

Ax2＋2Bxy＋Cy2＋2Dx＋2Ey＋F＝0，（*）

将坐标轴旋转θ角，求曲线Γ关于新坐标系x′Oy′的方程．

分析　将旋转公式④直接代入方程（*）．

解　将坐标轴旋转θ角，则

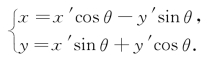
将这个旋转公式代入方程（*），得

A（x′cosθ－y′sinθ）2＋2B（x′cosθ－y′sinθ）（x′sinθ＋y′cosθ）＋C（x′sinθ＋y′cosθ）2＋2D（x′cosθ－y′sinθ）＋2E（x′sinθ＋y′cosθ）＋F＝0．

整理上式，得曲线Γ关于新坐标系x′Oy′的方程为

A′x′2＋2B′x′y′＋C′y′2＋2D′x′＋2E′y′＋F＝0．

其中A′＝Acos2θ＋2Bcosθsinθ＋Csin2θ，

B′＝－Asinθcosθ＋B（cos2θ－sin2θ）＋Csinθcosθ，

C′＝Asin2θ－2Bcosθsinθ＋Ccos2θ，

D′＝Dcosθ＋Esinθ，

E′＝Ecosθ－Dsinθ．

说明　本题的解答表明，曲线Γ关于新坐标系x′Oy′的方程中，常数项与方程（*）中的常数项相同，即旋转变换不会改变二次方程表达式中的常数项．同时，新方程中的二次项系数只与旋转角以及原方程中的二次项系数有关，而与原方程中的一次项系数及常数项无关．

由D′，E′的表达式还可以看到，如果方程（*）中有D＝E＝0，那么新方程中就有D′＝E′＝0．即如果原方程中不含一次项，那么通过旋转变换后所得的新方程中也不含一次项．