坐标轴的平移及其数学表达式

对于一个平面直角坐标系，不改变坐标轴的方向和单位长度，只改变原点的位置，这样的变换叫做坐标轴的平移，简称平移．

如图3-1，平面直角坐标系xOy经过平移，得到新坐标系x′O′y′；点O′在坐标系xOy中的坐标为（h，k）．

设点P在坐标系xOy和x′O′y′中的坐标分别为（x，y），（x′，y′），则由

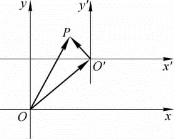
图3-1

得（x′，y′）＝（x，y）－（h，k），

或（x，y）＝（h，k）＋（x′，y′）．

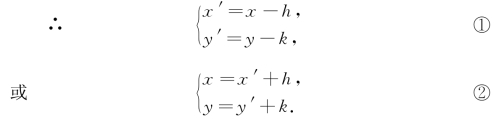
式①和②是关于坐标轴平移的坐标变换公式，简称平移公式．

利用公式①，可从点的旧坐标（x，y）求得它的新坐标（x′，y′）；利用公式②，则可从点的新坐标（x′，y′）求得它的旧坐标（x，y）．

例1　平移平面直角坐标系xOy，将原点O移到O′（2，－3），得到新坐标系x′O′y′．求：

（1）点A（5，3）和B（－4，0）的新坐标；

（2）直线l：y＝－5和曲线Γ：x2＋y2－4x＋6y＋8＝0关于新坐标系的方程．

分析　直接利用平移公式进行变换．

解　（1）由O′（2，－3），得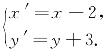

所以，点A（5，3）的新坐标为（5－2，3＋3），即（3，6）；

点B（－4，0）的新坐标为（－4－2，0＋3），即（－6，3）．

（2）由O′（2，－3），得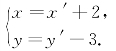

将这个平移公式代入直线l的方程中，得

y′－3＝－5，即y′＝－2；

再将这个平移公式代入曲线Γ的方程中，得

（x′＋2）2＋（y′－3）2－4（x′＋2）＋6（y′－3）＋8＝0．(www.xing528.com)

化简，得x′2＋y′2＝5．

所以，直线l关于坐标系x′O′y′的方程是

y′＝－2；

曲线Γ关于坐标系x′O′y′的方程是

x′2＋y′2＝5．

说明　已知一个点在旧坐标系中的坐标，可直接利用平移公式①来求出这个点的新坐标；而已知一条曲线关于旧坐标系的方程，则通常利用平移公式②，通过代换来求这条曲线关于新坐标系的方程．

通过平移变换，得到曲线Γ关于坐标系x′O′y′的方程是圆的标准方程．实际上，曲线Γ关于坐标系xOy的方程可变形为

（x－2）2＋（y＋3）2＝5，

可知O′（2，－3）正是⊙Γ的圆心．

直线l和⊙Γ如图3-2所示．

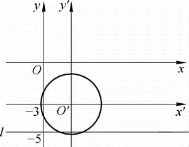
图3-2

例2　已知二次曲线Γ关于平面直角坐标系xOy的方程为

Ax2＋2Bxy＋Cy2＋2Dx＋2Ey＋F＝0，（*）

平移坐标系xOy，将原点移到O′（h，k），求曲线Γ关于新坐标系x′O′y′的方程．

分析　将平移公式②直接代入方程（*）．

解　平移坐标系xOy，将原点移到O′（h，k），则

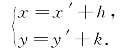
将这个平移公式代入方程（*），得

A（x′＋h）2＋2B（x′＋h）（y′＋k）＋C（y′＋k）2＋2D（x′＋h）＋2E（y′＋k）＋F＝0．

整理上式，得曲线Γ关于坐标系x′O′y′的方程为

Ax′2＋2Bx′y′＋Cy′2＋2（Ah＋Bk＋D）x′＋2（Bh＋Ck＋E）y′＋（Ah2＋2Bhk＋Ck2＋2Dh＋2Ek＋F）＝0．

说明　本题的解答表明，曲线Γ关于新坐标系x′O′y′的方程中，二次项的系数与方程（*）中二次项的系数对应相等，即平移变换不会改变二次方程表达式中二次项的系数．