圆锥曲线的切线方程及应用

如图2-15（1），直线l是⊙O的切线．在图2-15（2）中，直线l1，l2是曲线Γ的切线，但它们与Γ的公共点不止一个；而直线l3与Γ只有一个公共点，但l3不是曲线Γ的切线．

（1）平面曲线的切线　关于平面曲线的切线，一般的定义如下：设P是曲线Γ上一点，过点P引割线PQ，与曲线Γ交于另一点Q，使点Q沿着曲线Γ逐渐向点P靠拢，当Q与P重合时，直线PQ的新位置PT叫做经过曲线Γ上一点P的切线，如图2-16所示．

图2-16

（2）圆锥曲线的切线方程　下面，根据平面曲线的切线定义来探求圆锥曲线的切线方程．

首先探讨经过椭圆上一点P（x0，y0）的切线方程．

给定椭圆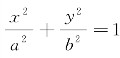上一点P（x0，y0），设Q（x1，y1）是这个椭圆上异于点P的另一个点，且不妨假定x1≠x0．

因为＝（x1－x0，y1－y0），所以割线PQ的方程为

（y1－y0）（x－x0）－（x1－x0）（y－y0）＝0．

在这个方程两边同乘以（y1＋y0），得

由点P，Q都在椭圆上，得

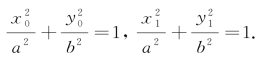
再将这两式相减，得，

即．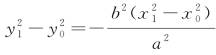

利用上式，可将方程化为

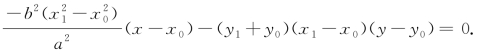
两边同除以（x1－x0），再整理得

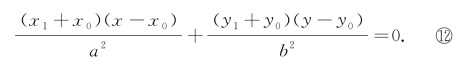
当点Q沿着椭圆移到与点P重合的位置时，则x1＝x0，y1＝y0．这时，割线PQ变成了经过点P的切线，方程就变为

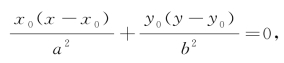
即

由点P在椭圆上，得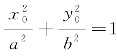，所以

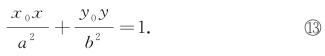
方程就是经过椭圆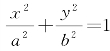上一点P（x0，y0）的切线方程．

其次探讨双曲线和抛物线的切线方程．

同样采用如上的方法，可以求得：

经过双曲线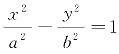上一点P（x0，y0）的切线方程是

经过抛物线y2＝2px上一点P（x0，y0）的切线方程是

y0y＝p（x＋x0）．

将上面所得椭圆、双曲线、抛物线的切线方程与这些曲线本身的标准方程进行比较，可以看到：

在圆锥曲线的标准方程中，如果分别用x0x，y0y替换其中的x2，y2，用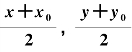分别替换其中的x，y，就得到经过此圆锥曲线上一点P（x0，y0）的切线方程．

通常，可利用这一替换法则来求圆锥曲线的切线方程．

如果椭圆的方程形如Ax2＋By2＝C（其中A，B，C同号），同样可用上述替换法则来求椭圆的切线方程．对于双曲线和抛物线，也是如此．

例7　求经过抛物线y2＝6x上一点的切线方程：(www.xing528.com)

（1）点O（0，0）；　（2）点P（2，－）．

分析　可直接利用替换法则写出切线的方程．

解　（1）经过抛物线y2＝6x上一点O（0，0）的切线方程是

即　x＝0．

（2）经过抛物线y2＝6x上一点P（2，－）的切线方程是

即　

说明　由本题（1）可知，经过抛物线y2＝ax（a≠0）的顶点O（0，0）的切线是y轴；同理，经过抛物线x2＝ay（a≠0）的顶点O（0，0）的切线是x轴．

例8　求经过椭圆2x2＋3y2＝5上一点A（－1，1）的切线方程．

分析　可直接利用替换法则写出切线的方程．

解　经过椭圆2x2＋3y2＝5上一点A（－1，1）的切线方程是

2·（－1）·x＋3·1·y＝5，

即　2x－3y＋5＝0．

说明　一般地，经过椭圆Ax2＋By2＝C（其中A，B，C同号）上一点P（x0，y0）的切线方程是Ax0x＋By0y＝C．

例9　已知：经过双曲线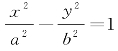（a＞0，b＞0）上一点P（x0，y0）的切线l与双曲线的两条渐近线分别相交于点M，N．

求证：点P平分线段MN．

分析　可利用代数方法来证明．先求出点M，N的坐标以及线段MN的中点坐标，再判断结论．

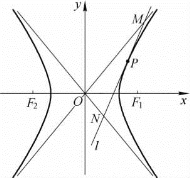
图2-17

证明　如图2-17，已知点P（x0，y0）在双曲线上，得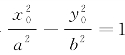，即（bx0＋ay0）（bx0－ay0）＝a2b2．

∵ab≠0，

∴bx0＋ay0≠0且bx0－ay0≠0．

经过双曲线上一点P（x0，y0）的切线l的方程是

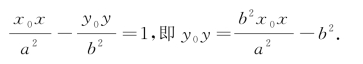
双曲线的两条渐近线的方程是．

解方程组得

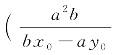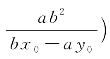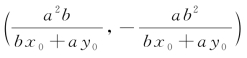可知点M，N的坐标分别为，和　之一．

因为

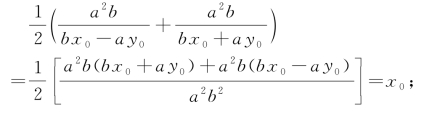
可知线段MN的中点坐标为（x0，y0）．

所以P（x0，y0）是线段MN的中点．

说明　通过本题的证明，得到双曲线的一个性质：夹在双曲线的两条渐近线之间的切线段被切点平分．