在探讨抛物线的标准方程⑤y2=2px时,利用了抛物线Γ的准线l′,并且知道方程⑤中的p是抛物线Γ的焦点F到准线l′的距离.
问题2-1 对于方程①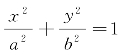 和方程③
和方程③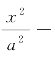
![]() =1分别表示的椭圆和双曲线,它们的准线方程分别是什么?
=1分别表示的椭圆和双曲线,它们的准线方程分别是什么?
分析 推导椭圆的标准方程①时已经指出,平面直角坐标系xOy中的x轴,其实就是圆锥面C的轴l在平面M内的射影l0.联系第1章关于圆锥曲线特征性质和统一性质的讨论,可知椭圆的两个焦点F1,F2都在x轴上,它的两条准线l1,l2都垂直于x轴;若设两条准线与x轴的垂足分别为T1,T2,则线段F1F2与线段T1T2都以坐标原点O为中点.由椭圆的标准方程①可知焦点F1,F2的坐标,于是可在平面直角坐标系xOy中探讨两条准线l1和l2的方程.
双曲线的情况类似.
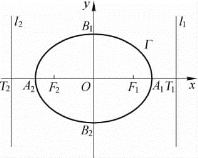
图2-10
研讨 如图2-10所示,对于方程①表示的椭圆Γ,其焦点F1和F2的坐标分别为(c,0)和(-c,0),其中![]() ;又知|F1F2|=2c.
;又知|F1F2|=2c.
椭圆的两条准线l1,l2都垂直于x轴.设 两 条 准线 与x轴 的垂足分别为T1,T2,则线段T1T2与线段F1F2的中点都是坐标原点O.
在第1章已得|F1F2|=e2|T1T2|,可知e2|OT1|=c,即![]() .再由
.再由![]() ,得
,得![]() .
.
所以,椭圆Γ的两条准线l1,l2的方程分别是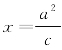 和
和![]() .
.
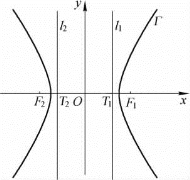
图2-11
对于方程③表示的双曲线Γ,如图2-11所示,它的焦点为F1,F2.注意到它的两条准线l1,l2同样垂直于x轴,设垂足分别为T1,T2,则坐标原点O同是线段T1T2与线段F1F2的中点,而且也有|F1F2|=2c,|F1F2|=e2|T1T2|,其中![]() .
.
因此,双曲线Γ的两条准线l1,l2的方程分别是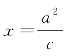 和
和![]() .
.
说明 由圆锥曲线的统一的特征性质可知,圆锥曲线上一点与焦点和相应准线的距离之比等于定值e.利用这一数量关系,还可进一步讨论圆锥曲线上一点与焦点的距离的表达式.
设P(x,y)是方程①所表示的椭圆Γ上的任意一点,可知点P与准线l1的距离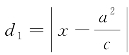 ,与准线l2的距离
,与准线l2的距离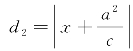 .又知若用|PF1|和|PF2|分别表示点P与焦点F1,F2的距离,则
.又知若用|PF1|和|PF2|分别表示点P与焦点F1,F2的距离,则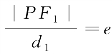 ,
,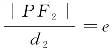 .于是,得
.于是,得
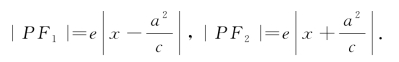
再由![]() ,得
,得
|PF1|=|a-ex|,|PF2|=|a+ex|,其中|x|≤a.
连接椭圆Γ上一点P与焦点F1(或F2)的线段PF1(或线段PF2)叫做点P的焦点半径.上面关于|PF1|和|PF2|的两个表达式,就是求方程①所表示的椭圆Γ上一点P的两条焦点半径长|PF1|和|PF2|的公式.
对于双曲线Γ上的任意一点P和双曲线的焦点F1,F2,我们同样将线段PF1和线段PF2叫做点P的焦点半径,并可得到求方程③所表示的双曲线Γ上一点P的焦点半径长的公式是:|PF1|=|a-ex|,|PF2|=|a+ex|,其中|x|≥a.
回到2.2节例3的讨论.对于双曲线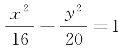 ,可知a=4,c=6,
,可知a=4,c=6,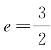 .设F1(6,0)和F2(-6,0),则此双曲线上一点P(x,y)的焦点半径长分别为
.设F1(6,0)和F2(-6,0),则此双曲线上一点P(x,y)的焦点半径长分别为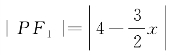 ,
,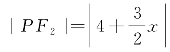 ,其中|x|≥4.于是,可知
,其中|x|≥4.于是,可知
当x≤-4时,|PF1|=![]() +4≥10,|PF2|=-
+4≥10,|PF2|=-![]() -4≥2;
-4≥2;
当x≥4时,|PF1|=![]() -4≥2,|PF2|=
-4≥2,|PF2|=![]() +4≥10.
+4≥10.
这时,由已知|PF1|=9,可知点P的坐标分量x满足条件x≥4,即点P在此双曲线的右支上;再由a=4可知|PF1|+|PF2|=8,得|PF2|=1或17,而当x≥4时|PF2|≥10,因此断定|PF2|=1应舍去,所以|PF2|=17是所求解.
由于抛物线的特征性质与圆锥曲线统一性质中有关抛物线的性质的表述一样,因此可以说推导抛物线的标准方程时利用了圆锥曲线的统一性质.于是提出:
问题2-2 能否利用圆锥曲线的统一性质,来推导椭圆和双曲线的方程?
分析 圆锥曲线统一性质中有关椭圆、双曲线的表述,同样指明它们都是平面内满足一定条件的动点的轨迹,当然可由此推导椭圆和双曲线的方程.
研讨 根据圆锥曲线的统一性质可知,椭圆是“平面内与一个定点和一条定直线的距离之比等于e且0<e<1的点的轨迹”.这个定点是椭圆的一个焦点,这条定直线是椭圆相应于这个焦点的准线.
在平面M内,已知椭圆Γ的左焦点为F2,相应的准线为l2,焦点F2到准线l2的距离为p(p>0).
经过焦点F2作准线l2的垂线,垂足为K2.以直线K2F2为x轴、![]() 的指向为x轴正向,以F2为原点并记作O,建立平面直角坐标系xOy,如图2-12所示.
的指向为x轴正向,以F2为原点并记作O,建立平面直角坐标系xOy,如图2-12所示.
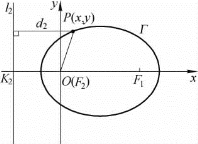
图2-12
在坐标系xOy中,焦点F2的坐标为(0,0),准线l2的方程为x=-p.
设P(x,y)是椭圆Γ上的任意一点,则
|PF2![]() ,P与准线l2的距离d2=|x+p|.
,P与准线l2的距离d2=|x+p|.
由|PF2|=ed2,得![]() .(https://www.xing528.com)
.(https://www.xing528.com)
化简,得
(1-e2)x2+y2-2pe2x-e2p2=0(其中0<e<1).⑨
方程⑨是椭圆Γ的方程,注意:此时坐标原点O是椭圆的左焦点,p是原点O即左焦点F2到相应准线l2的距离.
下面来推导双曲线的方程.
根据圆锥曲线的统一性质,可知双曲线是“平面内与一个定点和一条定直线的距离之比等于e且e>1的点的轨迹”.这个定点是双曲线的一个焦点,这条定直线就是双曲线相应于这个焦点的准线.
类似于推导椭圆的方程,在平面M内设双曲线Γ的右焦点为F1,相应的准线为l1,焦点F1与准线l1的距离为p(p>0),同样建立平面直角坐标系xOy,可得
(1-e2)x2+y2-2pe2x-e2p2=0(其中e>1).⑩
方程⑩是双曲线Γ的方程,注意:此时原点O是双曲线的右焦点,p是原点O即右焦点F1到相应准线l1的距离.
说明 利用圆锥曲线的统一性质推导出来的椭圆和双曲线的方程,它们的表达形式一样,但这样的方程表达式显然没有它们的标准方程简明.而且容易看出,方程⑨和⑩分别表示椭圆和双曲线,它们显然关于y轴不对称,关于原点O也不对称.因此必须清楚地认识到,对于曲线进行解析研究时,“适当地”建立平面直角坐标系有十分重要的意义.
例6 已知定点F和定直线l,点F到直线l的距离为p(p>0),点M在直线l上滑动,动点N在MF的延长线上且满足条件![]() .
.
(1)动点N的轨迹是什么图形?
(2)以经过F且垂直于l的直线为x轴,以F为原点且记作点O,建立平面直角坐标系xOy,然后求动点N的轨迹方程.
分析 (1)动点N满足的条件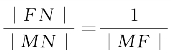 可变形为
可变形为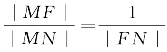 .注意到点F和点N在定直线l的同一侧,于是可考虑分别过点F,N作直线l的垂线,构建相似三角形从而导出新的比例关系式,并与圆锥曲线的统一的特征性质建立联系.
.注意到点F和点N在定直线l的同一侧,于是可考虑分别过点F,N作直线l的垂线,构建相似三角形从而导出新的比例关系式,并与圆锥曲线的统一的特征性质建立联系.
(2)在平面直角坐标系xOy中,将已知条件用坐标或坐标关系式表示出来,再探求点N的坐标应满足的关系式.
解 (1)如图2-13,分别过点F,N作定直线l的垂线,垂足分别为K和T,可证得△MFK∽△MNT.
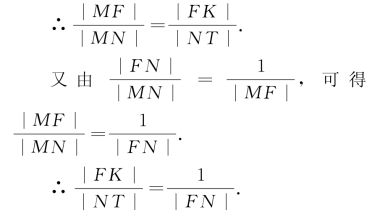
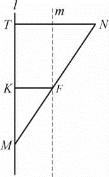
图2-13
这个比例式可改写为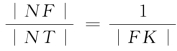 ,又知
,又知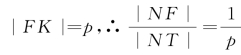 .
.
比例式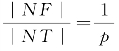 表示动点N与定点F和定直线l的距离之比等于常数
表示动点N与定点F和定直线l的距离之比等于常数![]() .又知动点N一定在经过点F且平行于l的直线m的右侧.因此,若设
.又知动点N一定在经过点F且平行于l的直线m的右侧.因此,若设![]() ,则
,则
①当p>1即0<e<1时,动点N的轨迹是一个椭圆在直线m右侧的部分;
②当0<p<1即e>1时,动点N的轨迹是一条双曲线在直线m右侧的部分;
③当p=1即e=1时,动点N的轨迹是一条抛物线在直线m右侧的部分.
(2)如图2-14,在平面直角坐标系xOy中,y轴与直线l平行.
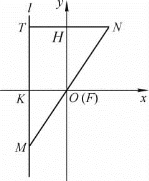
图2-14
设点N的坐标为(x,y).由点M在直线l上滑动、点N在MF的延长线上,可知点N一定在y轴的右侧,即x>0.
同(1)可得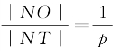 .
.
∵|NO|=![]() ,|NT|=x+p,
,|NT|=x+p,
![]()
整理得,动点N的轨迹方程为
(p2-1)x2+p2y2-2px-p2=0(x>0).
说明 在(1)中对动点N的轨迹进行判断时,利用了圆锥曲线的统一的特征性质;在(2)指定的平面直角坐标系xOy中,求出了动点N的轨迹方程.
一般而言,曲线的方程(即曲线的代数表示形式)是与选取的坐标系有关的,而曲线的几何形态则与选取的坐标系无关.由(1)已经知道,动点N的轨迹是圆锥曲线的一部分,具体情况与p值的大小有关;由(2)导出了动点N的轨迹方程,可知这个方程应是(1)中所述的轨迹在平面直角坐标系xOy中的代数表示形式.因为(2)中的平面直角坐标系xOy不是建立在“标准位置”上,所以得到的轨迹方程没有呈现为椭圆或双曲线、抛物线的标准方程的形式.但是,(2)导出的轨迹方程显然是一个二元二次方程,关于圆锥曲线与二元二次方程之间的联系,留待第3章再进行研讨.
在前面推导圆锥曲线的标准方程时,按照所建立的平面直角坐标系xOy的不同情况,圆锥曲线在直角坐标系中的位置特征及其标准方程的表达式也不同.
关于圆锥曲线标准方程的各种表达形式,归纳如表所示:

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




