抛物线的几何性质及其对称性分析

根据抛物线的标准方程⑤y2＝2px（p＞0），现探讨抛物线的几何性质．

（1）范围　由方程y2＝2px中p＞0可知，设抛物线Γ上一点P的坐标为（x，y），则坐标分量x适合不等式x≥0．这说明抛物线Γ经过原点且在y轴右侧．又知当x的值增大时，｜y｜也随之增大，说明抛物线Γ向右上方和右下方无限延伸，如图2-8所示．

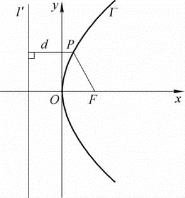
图2-8

（2）对称性　在方程⑤中，用－y代替y，方程⑤不变，说明抛物线Γ关于x轴对称．抛物线的对称轴叫做抛物线的轴．

（3）顶点　抛物线与它的轴的交点叫做抛物线的顶点．在方程⑤中，当y＝0时，x＝0，说明坐标原点O（0，0）是抛物线Γ的顶点．

（4）离心率　抛物线上的点到焦点的距离和它到准线的距离之比叫做抛物线的离心率．根据抛物线的特征性质可知，抛物线的离心率等于1，用e表示为e＝1．

说明　抛物线的焦点与顶点的距离称为抛物线的焦距，通常用f表示．在抛物线Γ的标准方程y2＝2px中，常数p表示焦点到准线的距离（可称为焦参数），现在可以说p的几何意义就是p＝2f．

抛物线的离心率e＝1，即抛物线Γ上的任意一点P（x，y）与焦点F的距离｜PF｜等于点P与准线l′的距离d′，所以．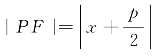

连接抛物线Γ上一点P与焦点F的线段PF叫做点P的焦点半径．抛物线y2＝2px（p＞0）上一点P（x，y）的焦点半径长用公式表示为．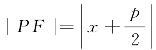

例5　过抛物线y2＝2px（p＞0）的焦点F的一条直线与此抛物线交于P，Q两点，经过点P和抛物线顶点的直线与准线交于点M．求证：直线MQ平行于此抛物线的对称轴．

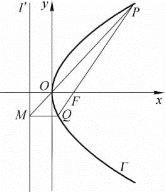
图2-9

分析　已知抛物线的标准方程，可知此抛物线的焦点坐标和顶点坐标，以及准线方程和对称轴方程．

解　如图2-9所示，抛物线y2＝2px（p＞0）的焦点F的坐标是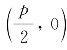，准线方程是，顶点是原点O（0，0）；对称轴是x轴，其方程是y＝0．

已知点P在抛物线y2＝2px（p＞0）上，不妨设点P的坐标为（t，），其中t≥0，则过点P和焦点F的直线PF的方程是

即．(www.xing528.com)

由方程组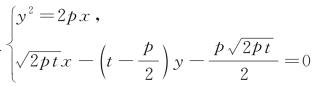得

解方程，得

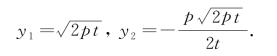
其中y1是点P的纵坐标，y2是点Q的纵坐标．

过点P（t，）和顶点O（0，0）的直线PO的方程是

由方程组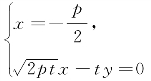得

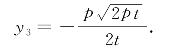
于是，得y3＝y2，其中y3是点M的纵坐标．

若设P（t，），同理，得y3＝y2．

所以，对于P（x1，y1），Q（x2，y2），M（x3，y3）三点，由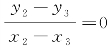，可知直线MQ平行于x轴，即MQ平行于此抛物线的对称轴．

说明　本题的证明采用了解析法．在证明过程中，注意到抛物线及其准线都是关于x轴对称的，可知若设点P的坐标为（t，），这时求点M的纵坐标y3的过程与点P坐标为（t，）的情况类似，而且应得．还有，由于直线MQ是否与抛物线的对称轴平行取决于M，Q的纵坐标是否相等，因此解方程组时不必求出未知数x的值．

另外，也可考虑用其他思路来证明直线MQ与抛物线的对称轴平行．例如，求出y2以后，可设点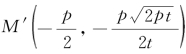，那么点M′在抛物线的准线上，且M′Q与抛物线的对称轴平行．

已知点P（t，），顶点O（0，0），则由

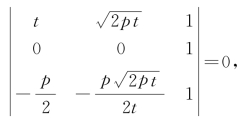
可知P，O，M′三点共线．因为直线PO与抛物线的准线的交点唯一，可知点M′与点M重合，所以直线MQ与抛物线的对称轴平行．