根据双曲线Γ的标准方程 ,b>0),现对双曲线的几何性质进行系统地探讨和整理.
,b>0),现对双曲线的几何性质进行系统地探讨和整理.
(1)范围 由方程③可知,设双曲线Γ上一点P的坐标为(x,y),则坐标分量x适合不等式![]() ,得x≥a或x≤-a.这说明双曲线Γ位于两条平行直线x=a和x=-a所夹区域的外部,如图2-4所示.
,得x≥a或x≤-a.这说明双曲线Γ位于两条平行直线x=a和x=-a所夹区域的外部,如图2-4所示.
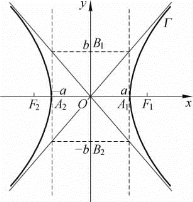
图2-4
(2)对称性 方程③表明,它所表示的双曲线Γ分别关于y轴、x轴和原点对称.这时,坐标轴是双曲线Γ的对称轴,原点O是双曲线Γ的对称中心.
双曲线的对称中心叫做双曲线的中心.
(3)顶点 在方程③中,令y=0,得x=±a,这说明A1(a,0)和A2(-a,0)是双曲线Γ与x轴的两个交点;令x=0,可知方程③没有实数解,这说明双曲线Γ与y轴不相交.双曲线与它的一条对称轴的交点叫做双曲线的顶点,双曲线有两个顶点.
对于双曲线Γ,A1,A2是它的顶点,线段A2A1叫做双曲线Γ的实轴.为了便于观察双曲线Γ的图形特征,画图时通常也在y轴上标出B1(0,b)和B2(0,-b),并把线段B1B2叫做双曲线Γ的虚轴.|A2A1|=2a,|B2B1|=2b,a和b分别叫做双曲线Γ的实半轴长和虚半轴长.
(4)渐近线 在图2-4中分别作两组平行线x=±a和y=±b,则这四条直线围成一个矩形,这个矩形的两条对角线所在直线的方程分别是![]() 和
和![]() .
.
观察方程③表示的双曲线Γ,它的两支向上侧或下侧无限延伸,且与直线![]() 和直线
和直线![]() 逐渐接近.可以证明:双曲线Γ在第一象限内那一部分在直线
逐渐接近.可以证明:双曲线Γ在第一象限内那一部分在直线![]() 的下方,并随着x逐渐增大而与直线
的下方,并随着x逐渐增大而与直线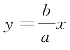 越来越接近;在第四象限内那一部分在直线
越来越接近;在第四象限内那一部分在直线![]() 的上方,并随着x逐渐增大而与直线
的上方,并随着x逐渐增大而与直线![]() 越来越接近.双曲线Γ在第二、三象限的情况,与它在第一、四象限的情况类似.我们把直线
越来越接近.双曲线Γ在第二、三象限的情况,与它在第一、四象限的情况类似.我们把直线 和直线
和直线![]() 叫做双曲线Γ的渐近线.
叫做双曲线Γ的渐近线.
(5)离心率 双曲线的焦距与实轴长的比叫做双曲线的离心率.对于方程③所表示的双曲线Γ,它的离心率等于![]() .在圆锥曲线的统一性质中,曾用e表示圆锥曲线上一点与一个定点和一条定直线的距离之比的比值,又知对于双曲线Γ有c=ae,可见这个比值e就是双曲线Γ的离心率.所以,双曲线Γ的离心率可表示为
.在圆锥曲线的统一性质中,曾用e表示圆锥曲线上一点与一个定点和一条定直线的距离之比的比值,又知对于双曲线Γ有c=ae,可见这个比值e就是双曲线Γ的离心率.所以,双曲线Γ的离心率可表示为![]() ,且e>1.
,且e>1.
由![]() 和c2=a2+b2,得
和c2=a2+b2,得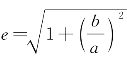 ,可知
,可知![]() 越大则e越大,
越大则e越大,![]() 越小则e越小.因为直线
越小则e越小.因为直线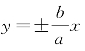 是双曲线Γ的渐近线,所以
是双曲线Γ的渐近线,所以![]() 的大小决定双曲线Γ的陡峭程度,即e的大小决定双曲线Γ的陡峭程度.一般地,e越大则双曲线越陡.这是因为e越大即
的大小决定双曲线Γ的陡峭程度,即e的大小决定双曲线Γ的陡峭程度.一般地,e越大则双曲线越陡.这是因为e越大即![]() 越大,这时由渐近线
越大,这时由渐近线![]() 所夹的内部含有x轴的那两个部分的张口也越大,所以双曲线Γ越陡.
所夹的内部含有x轴的那两个部分的张口也越大,所以双曲线Γ越陡.
说明 由c2-a2=b2,可知a(实半轴的长)、b(虚半轴的长)、c(半焦距)三者满足关系式a2+b2=c2.●
例3 已知双曲线 的两个焦点为F1,F2,点P在双曲线上,|PF1|=9,求|PF2|.
的两个焦点为F1,F2,点P在双曲线上,|PF1|=9,求|PF2|.
分析 可利用点P在双曲线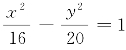 上以及|PF1|=9列出两个方程,通过解方程组来确定点P的坐标,然后求出|PF2|.
上以及|PF1|=9列出两个方程,通过解方程组来确定点P的坐标,然后求出|PF2|.
解 由双曲线 ,得a=4,b=
,得a=4,b=![]() ,c=6.
,c=6.
根据双曲线的对称性,不妨设两个焦点为F1(6,0),F2(-6,0).
设点P(x,y)在双曲线![]() 上,则
上,则![]() 20,坐标分量x的取值范围是x≤-4或x≥4.
20,坐标分量x的取值范围是x≤-4或x≥4.
又 知![]() ,|P F2|=
,|P F2|=![]() .
.
由|PF1|=9,即![]() ,得
,得
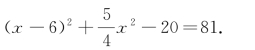
再整理,得9x2-48x-260=0.
解方程,得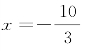 或
或![]() .
.
由于![]() 不在点P的坐标分量x的取值范围内,因此舍去.
不在点P的坐标分量x的取值范围内,因此舍去.
另一根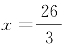 在点P的坐标分量x的取值范围内.
在点P的坐标分量x的取值范围内.
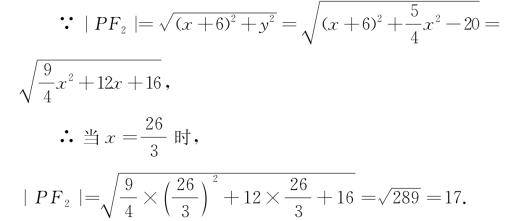
说明 双曲线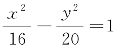 中,a=4.根据双曲线的特征性质可知,双曲线上一点P满足条件|PF1|-|PF2|=±8.题中给定|PF1|=9,容易推出|PF2|=1或17.必须注意,如此利用双曲线的特征性质求解时,要进一步判断究竟有两解、还是应取一解(若给定条件不当还有可能无解).仍设双曲线
中,a=4.根据双曲线的特征性质可知,双曲线上一点P满足条件|PF1|-|PF2|=±8.题中给定|PF1|=9,容易推出|PF2|=1或17.必须注意,如此利用双曲线的特征性质求解时,要进一步判断究竟有两解、还是应取一解(若给定条件不当还有可能无解).仍设双曲线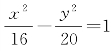 的两个焦点为F1(6,0)和F2(-6,0),此曲线上一点为P(x,y),可知x≤-4或x≥4.
的两个焦点为F1(6,0)和F2(-6,0),此曲线上一点为P(x,y),可知x≤-4或x≥4.
①若![]() ,得(https://www.xing528.com)
,得(https://www.xing528.com)
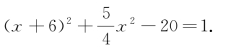
再整理,得![]() .
.
解方程,得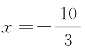 或x=-2.
或x=-2.
由于这两个根都不在点P的坐标分量x的取值范围内,可知此双曲线上不存在点P使|PF2|=1.
②若![]() ,得
,得
![]()
再整理,得3x2+16x-364=0.
解方程,得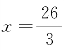 或x=-14.
或x=-14.
这两个根都在点P的坐标分量x的取值范围内.
当![]() 时,由
时,由
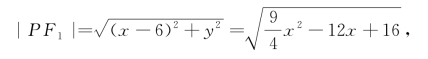
得 ,符合题意.
,符合题意.
因此,可取|PF2|=17.(当x=-14时,由|PF1|= 可知|PF1|≠9,即x=-14不合题意,但没有必要讨论.)
可知|PF1|≠9,即x=-14不合题意,但没有必要讨论.)
如上所述判断过程有些繁琐,后面再留意尽可能改用更简方法来讨论这个问题.
例4 如图2-5所示,A,B,C是三个观察哨,A在B的正东,两地相距6km;C在B的北偏西30°,两地相距4km.在某一时刻,A观察哨发现有一种信号,并知道该信号的传播速度是1km/s;4s后B,C两个哨所同时发现这种信号.现用P表示发出信号的地点,试通过建立平面直角坐标系xOy和指出点P的坐标,以确定这一信号发出地点的位置.
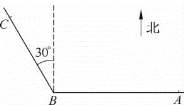
图2-5
分析 信号从点P发出以后,到达哨所A和B的时间差是4s,由信号的传播速度可知|PB|与|PA|的差,于是可断定点P位于以A,B为焦点的双曲线中内部含焦点A的一支上.又由B,C两个哨所同时发现信号,可知|PB|=|PC|,即点P在线段BC的垂直平分线上.建立适当的平面直角坐标系,可求出点P所在的双曲线及直线的方程;联立方程组,可求出点P的坐标.
解 以经过A,B两点的直线为x轴,线段AB的垂直平分线为y轴,1km为单位长度,建立平面直角坐标系xOy,如图2-6所示.
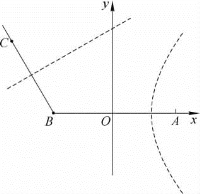
图2-6
在平面直角坐标系xOy中,A和B的坐标分别为(3,0)和(-3,0).已知信号从点P发出以后,到达哨所A和B的时间差是4s,又知该信号的传播速度是1km/s,得|PB|-|PA|=4,可知点P在以A,B为焦点的双曲线中内部含焦点A的那一支上.
因为双曲线的半焦距c=3,实半轴长a=2,又由b2=c2-a2得b2=5,所以点P所在双曲线的方程是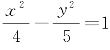 ,其中内部含焦点A的那一支满足条件x≥2.
,其中内部含焦点A的那一支满足条件x≥2.
已知信号从点P发出以后,B,C两个哨所同时发现信号,得|PB|=|PC|,所以点P在线段BC的垂直平分线上.由哨所B,C的位置,得B(-3,0),![]() ,则线段BC的垂直平分线的方程是
,则线段BC的垂直平分线的方程是![]() .
.
由方程组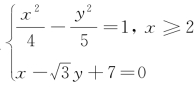 , 解得
, 解得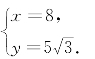
所以,点P的坐标是(8,![]() ).
).
说明 根据已知条件,可断定点P在双曲线的右支上、又在一条线段的垂直平分线上.这是本题的解题关键所在.我们要熟悉一些曲线(直线)的特征性质,并学会灵活应用.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




