【摘要】:在平面M内,已知双曲线Γ的两个焦点分别为F1,F2,|F1F2|=2c,定长m=2a,其中0<a<c.图2-3以线段F1F2所在的直线为x轴、的指向为x轴正向,且以线段F1F2的中点O为原点,建立平面直角坐标系xOy,如图2-3所示.在平面直角坐标系xOy中,F1(c,0),F2(-c,0).设P(x,y)是双曲线Γ上任意一点,则由||PF1|-|PF2||=2a,得化简,得(c2-a2)x2-a
在平面M内,已知双曲线Γ的两个焦点分别为F1,F2,|F1F2|=2c,定长m=2a,其中0<a<c.
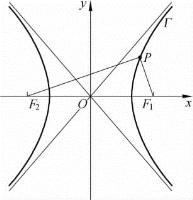
图2-3
以线段F1F2所在的直线为x轴、![]() 的指向为x轴正向,且以线段F1F2的中点O为原点,建立平面直角坐标系xOy,如图2-3所示.
的指向为x轴正向,且以线段F1F2的中点O为原点,建立平面直角坐标系xOy,如图2-3所示.
在平面直角坐标系xOy中,F1(c,0),F2(-c,0).
设P(x,y)是双曲线Γ上任意一点,则
![]()
由||PF1|-|PF2||=2a,得
![]()
化简,得
(c2-a2)x2-a2y2=a2(c2-a2).
∵0<a<c,∴c2-a2>0.(https://www.xing528.com)
设c2-a2=b2,且b>0,得
b2x2-a2y2=a2b2,
即
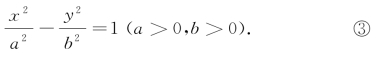
方程③称为双曲线的标准方程,其中b2=c2-a2.这个方程所表示的双曲线Γ,它的两个焦点在x轴上,焦点是F1(c,0)和F2(-c,0).
说明 我们通过建立平面直角坐标系xOy,利用双曲线的特征性质导出了双曲线的标准方程.如同椭圆的情况一样,平面直角坐标系xOy中的x轴,其实就是第1章中圆锥面C的轴l在平面M内的射影l0,双曲线的两个焦点都在x轴上,即在l0上.
同样地,双曲线的两个焦点的距离叫做焦距.
本节设双曲线的焦距|F1F2|=2c,定长m=2a,联系圆锥曲线统一性质中这条双曲线的e(这时e>1),可知|F1F2|=me,即2a·e=2c,得c=ae.
在探求双曲线方程时,如果以线段F1F2所在的直线为y轴、线段F1F2的中点O为原点,相应地建立平面直角坐标系xOy,使F1(0,c),F2(0,-c),那么可导出双曲线的方程为
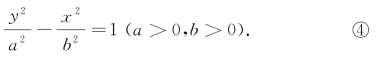
方程④也是双曲线的标准方程.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




