椭圆的几何性质及对称性探讨

根据椭圆Γ的标准方程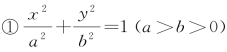），现对椭圆的几何性质进行系统地探讨和整理．

图2-2

（1）范围　由方程①可知，设椭圆Γ上一点P的坐标为（x，y），则坐标分量x，y分别适合不等式

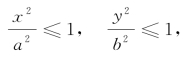
得｜x｜≤a，｜y｜≤b．这说明椭圆Γ位于直线x＝±a和直线y＝±b所围成的矩形里，如图2-2所示．

（2）对称性　在方程①中，把x换成－x，或把y换成－y，或把x和y相应地同时换成－x和－y，可知方程①都不变．这说明椭圆Γ分别关于y轴、x轴和原点对称．这时，坐标轴是椭圆Γ的对称轴，原点O是椭圆Γ的对称中心．

椭圆的对称中心叫做椭圆的中心．

（3）顶点　在方程①中，令y＝0，得x＝±a；令x＝0，得y＝±b．这说明A1（a，0）和A2（－a，0）是椭圆Γ与x轴的两个交点，B1（0，b）和B2（0，－b）是椭圆Γ与y轴的两个交点．椭圆与它的对称轴的交点叫做椭圆的顶点，一个椭圆有四个顶点，这里的A1，A2和B1，B2都是椭圆Γ的顶点．

以椭圆的同一条对称轴上的两个顶点为端点的线段叫做椭圆的长轴或短轴．线段A2A1和线段B2B1分别是椭圆Γ的长轴和短轴，｜A2A1｜＝2a，｜B2B1｜＝2b，a和b分别叫做椭圆的长半轴长和短半轴长．

（4）离心率　椭圆的焦距与长轴长的比叫做椭圆的离心率．对于方程①所表示的椭圆Γ，它的离心率等于．在圆锥曲线的统一性质中，曾用e表示圆锥曲线上一点与一个定点和一条定直线的距离之比的比值，又知对于椭圆Γ有c＝ae，可见这个e就是椭圆Γ的离心率．所以，椭圆Γ的离心率可表示为，且0＜e＜1．

由和c2＝a2－b2，得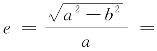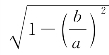，可知越小则e越大，越大则e越小．因为的大小决定椭圆的扁平程度，所以e的大小决定椭圆的扁平程度．e越大，可知越小，即b相对于a越小，则椭圆越扁．

说明　由a2－c2＝b2，可知a（长半轴的长）、b（短半轴的长）、c（半焦距）三者满足关系式a2＝b2＋c2．

例1　已知椭圆的焦距是12，离心率是0．6，求在平面直角坐标系xOy中这个椭圆的标准方程．

分析　椭圆的标准方程中有a，b两个数待定，在a，b，c，e四个量中知其中两个可求其余两个．

解　已知椭圆的焦距2c＝12即c＝6，离心率e＝0．6，由，得a＝10．再由b2＝a2－c2，得b2＝102－62＝64．所以(www.xing528.com)

当椭圆的焦点在x轴上时，它的标准方程是

当椭圆的焦点在y轴上时，它的标准方程是

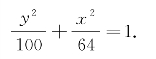
说明　在平面直角坐标系xOy中，根据椭圆的焦点在x轴上还是在y轴上，它相应的标准方程有不同的表示形式，所以本题有两个答案．

例2　已知椭圆的两个焦点为F1，F2，点P在这个椭圆上，且使△PF1F2是一个直角三角形．设｜PF1｜＞｜PF2｜，求｜PF1｜，｜PF2｜．

分析　已知这个椭圆的标准方程，可得到椭圆的长轴长和焦距．由△PF1F2是一个直角三角形，可列出关于｜PF1｜，｜PF2｜的方程组．

解　由椭圆的方程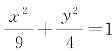，可知a＝3，b＝2，c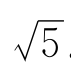＝．于是，得椭圆的长轴长2a＝6，焦距，即｜PF1｜＋｜PF2｜＝6，｜F1F2｜＝．

因为△PF1F2是直角三角形，｜PF1｜＞｜PF2｜，所以

①若边F1F2是Rt△PF1F2的斜边，则

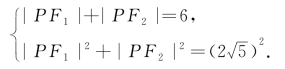
解方程组，得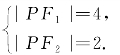

②若边F1F2是Rt△PF1F2的直角边，则

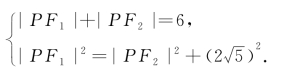
解方程组，得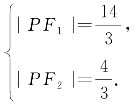

说明　根据题意，在Rt△PF1F2中，边F1F2可能是斜边，也可能是直角边．如果边F1F2是直角边，又知｜PF1｜＞｜PF2｜，那么这个直角三角形的斜边一定是PF1．