圆锥曲线的特征量解析

在圆锥曲线的统一性质中，涉及位于圆锥曲线所在平面内的一个定点和一条定直线（即圆锥曲线的一个焦点及相应准线）．在已经给定圆锥面C及截平面M的情况下，相关定点和定直线也可利用一个Dandelin球来定位．

问题1-2　在给定圆锥面C［A；l，θ］及不经过点A的截平面M的情况下，圆锥曲线统一性质中的定点和定直线的位置，能否利用数量关系来定量地描述？

分析　圆锥面C是由顶点A及母线与轴l的夹角大小确定的．而平面M的位置，可由平面M与轴l所成角的大小以及平面M上一点与顶点A的距离来确定．于是本问题归结为：能否利用分别对圆锥面C及平面M具有“确定”意义的量所构成的数量关系式，来描述圆锥曲线统一性质中的定点和定直线的位置．

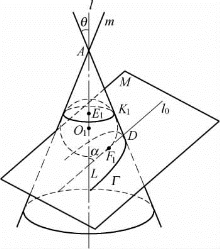
图1-14

研讨　如图1-14所示，给定圆锥面C［A；l，θ］，设轴l与平面M所成的角为α，0≤α＜，轴l在平面M内的射影为直线l0，l0与l交于点L；取l0与圆锥面C一条母线的交点D，它使∠ALD＝α．再设｜AD｜＝d，d＞0．

这时，平面M的位置由α和d的大小确定，则由平面M与圆锥面C相截所得的圆锥曲线Γ也完全确定．

作球O1，使它与圆锥面C及平面M都相切，可知球心O1在轴l上．设球O1与平面M的切点是F1，则点F1在直线l0上；又设球O1与圆锥面C的切点圆是⊙E1，母线AD与⊙E1相交于点K1；⊙E1所在的平面N与平面M的交线是l1，直线l0与l1相交于点T1．可知F1，l1分别是圆锥曲线Γ特征性质中的定点和定直线，轴l⊥平面N．

经过直线l0与轴l作平面S，由于l0是l在平面M内的射影，可知平面S⊥平面M；又由l⊥平面N，得平面S⊥平面N．所以，平面N与平面M的交线l1垂直于平面S，得l0⊥l1，点T1是垂足．

在平面S内，相关的直线和点的位置如图1-15所示．图中，L是l0与l的交点，∠LAD＝θ，∠ALD＝α，∠O1DF1＝∠O1DK1，O1F1⊥LD，O1K1⊥AD，还可知∠ADT1＝α＋θ，｜O1F1｜＝｜O1K1｜；又知｜AD｜＝d，｜DF1｜＝｜DK1｜．

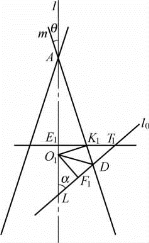
图1-15

设｜DF1｜＝x，得｜DK1｜＝x，｜AK1｜＝d－x．

Rt△AO1K1和Rt△DO1K1有公共边O1K1．

在Rt△AO1K1中，｜O1K1｜＝｜AK1｜tan∠O1AK1＝（d－x）tanθ；

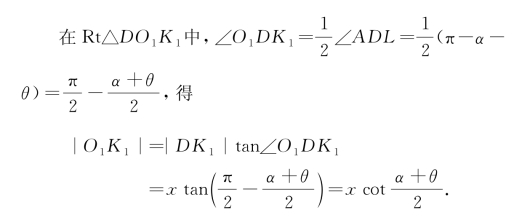
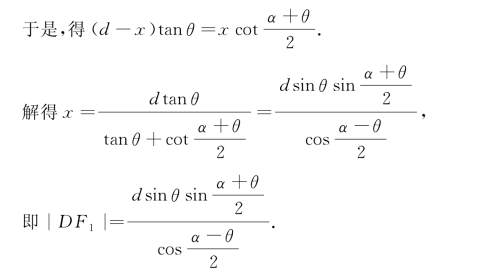
由｜DF1｜以及点F1在线段LD上，可确定F1的位置．

下面探讨关于直线l1的位置的定量描述．

因为点D是l0与圆锥面C一条母线的交点，即点D是平面M与圆锥面C的一个公共点，所以点D在圆锥曲线Γ上．又知｜DT1｜是点D到直线l1的距离，可知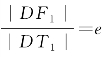．于是，得

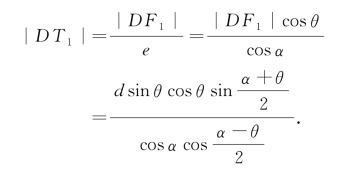
由｜DT1｜以及点T1在线段LD的延长线上，可确定T1的位置；又知直线l1在平面M上，它经过点T1且与l0垂直，因此可确定直线l1的位置．

再对上面所得的结论深入研究，以进一步揭示有关数量关系的特征．

（1）当α＝θ时，圆锥曲线Γ是抛物线．由于这时只能作一个球O与圆锥面C及平面M都相切，因此相应的定点和定直线分别是唯一的．不妨设这个定点为F，定直线为l′，直线l′与轴l在平面M内的射影l0的交点为T，则

｜DF｜＝｜DT｜＝dsin2θ．

（2）当θ＜α＜时，圆锥曲线Γ是椭圆．这时还可在平面M的另一侧作一个球O2与圆锥面C及平面M都相切．设球O2与平面M相切的切点是F2；球O2与圆锥面C相切所得的切点圆是⊙E2；直线l0与圆锥面C的另一条母线相交于点D′，母线AD′与⊙E2相交于点K2；⊙E2所在的平面N′与平面M的交线是l2，直线l0与l2相交于点T2．其中的F2，l2也分别是圆锥曲线Γ特征性质中的定点和定直线．

设｜AD′｜＝d′，可知｜AK2｜＝d′＋｜D′K2｜．在平面S中，同样指出相关的直线和点的位置，如图1-16所示．

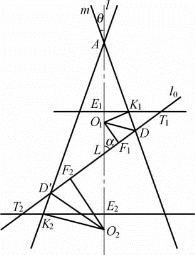
图1-16

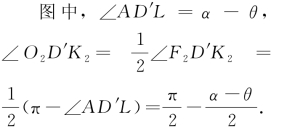
类似于求｜DK1｜那样，利用Rt△AK2O2和Rt△O2K2D′中的公共边O2K2，得

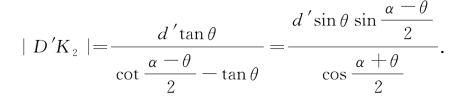
在△AD′D中，由正弦定理，得

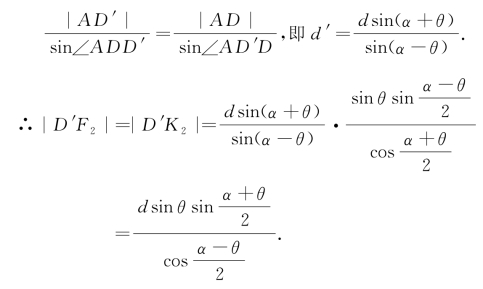
还可求得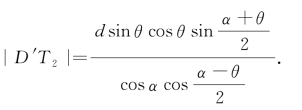

所以，点T2和直线l2的位置可以确定，且知

（3）当0≤α＜θ时，圆锥曲线Γ是双曲线．这时，还可在圆锥面C的另一支内作一个球O2与圆锥面C及平面M都相切．设球O2与平面M的切点是F2；球O2与圆锥面C的切点圆是⊙E2；直线l0与圆锥面C的另一条母线相交于点D′，母线AD′与⊙E2相交于点K2；⊙E2所在的平面N′与平面M的交线是l2，直线l0与l2相交于点T2．其中的F2，l2也分别是圆锥曲线Γ特征性质中的定点和定直线．

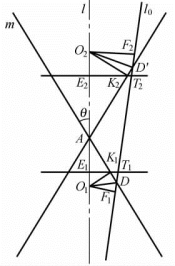
图1-17

设线段｜AD′｜＝d′，可知｜AK2｜＝d′－｜D′K2｜．

如图1-17所示，在平面S中，同样指出相关的直线和点的位置．图中，∠AD′D＝θ－α．

与（2）的讨论类似，得

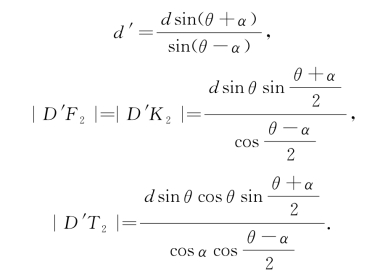
所以，点T2和直线l2的位置可以确定，且知

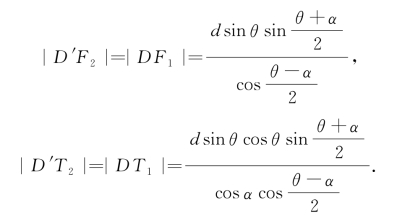
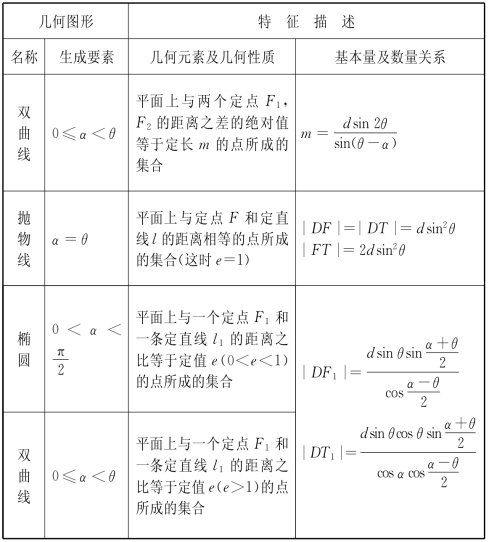
说明　本问题研究所得的结论中涉及三个几何量：圆锥面C的母线与轴l的夹角θ，轴l与平面M所成的角α，线段AD的长度d．不妨将θ，α，d称为确定圆锥面C与平面M相对位置的基本量，则圆锥曲线的统一性质中的定点和定直线的位置可用这三个基本量构成的数量关系式来定量地描述．

根据圆锥曲线的统一性质，可知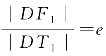，利用这个关系式，可将｜DF1｜与｜DT1｜相互表示．同理，｜DF2｜与｜DT2｜也可相互表示．

通过问题1-2的研讨可知，那些确定圆锥面C及其与平面M相对位置的基本量θ，α，d，对于相应圆锥曲线的几何特征也具有“确定”的意义．于是进一步提出：

问题1-3　椭圆和双曲线的特征性质中的定长m，是否能用关于基本量θ，α，d的数量关系式来表示？

分析　可参照问题1-2的研讨过程，把本问题转化为平面图形中的度量关系问题．

研讨　（1）求椭圆特征性质中的定长m．设轴l在平面M内的射影为直线l0，直线l0与轴l相交于点L，直线l0与圆锥面C的两条母线分别相交于点D，D′，∠ALD＝α，｜AD｜＝d．

经过相交直线l和l0作平面S，如图1-18所示．图中F1，F2是椭圆特征性质中的两个定点．

由于D是椭圆上一点，根据椭圆的特征性质，可知定长m＝｜DF1｜＋｜DF2｜．

∵｜D′F2｜＝｜DF1｜，

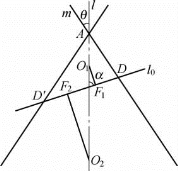
图1-18

∴m＝｜DF1｜＋｜DF2｜＝｜D′F2｜＋｜DF2｜＝｜D′D｜．

在△AD′D中，∠D′AD＝2θ，∠AD′D＝α－θ．由正弦定理，可知

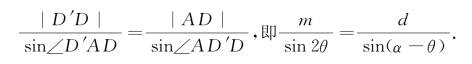
于是，得．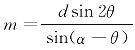

图1-19

（2）求双曲线特征性质中的定长m．同（1）所设，经过相交直线l和l0作平面S，如图1-19所 示．图 中F1，F2是双曲线特征性质中的两个定点，｜AD｜＝d．

由于D，D′是双曲线上的点，不妨设｜DF2｜＞｜DF1｜，根据双曲线的特征性质，可知定长m＝｜DF2｜－｜DF1｜（或m＝｜D′F1｜－｜D′F2｜）．

∵｜D′F2｜＝｜DF1｜，

∴m＝｜DF2｜－｜D′F2｜＝｜DD′｜．

在△ADD′中，∠DAD′＝π－2θ，∠AD′D＝θ－α．

利用正弦定理，得．

说明　给定基本量θ，α，d，则圆锥曲线特征性质中有关的定点和定直线的位置以及定长的大小都可用由θ，α，d确定的数量关系来描述．

将前面讨论所得的结论进行整理，如表所示：

（续表）

下面，再来讨论与圆锥曲线有关的一些特殊线段．

问题1-4　已知圆锥面C［A；l，θ］，平面M不经过点A，轴l与平面M交于点L，它们所成的角为α且0＜α＜；平面M与圆锥面C的截线为Γ．在连接点A与截线Γ上任意一点的线段中，最短的线段在什么位置？

分析　连接点A与截线Γ上任意一点的线段位于圆锥面C的母线上，它们与轴l的夹角都等于θ．

研讨　设P是截线Γ上任意一点，则直线AP是圆锥面C的母线，可知线段AP与AL的夹角为θ．

在轴l与母线AP确定的平面上作△ALP，如图1-20所示．

在△ALP中，∠LAP＝θ．设∠ALP＝β，则∠APL＝π－（θ＋β）．由正弦定理，得

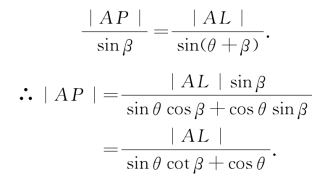
图1-20

在上式中，0＜β＜π，β的大小与点P在Γ上的位置有关．由于cotβ在区间（0，π）内是减函数，而｜AL｜，sinθ和cosθ都是确定的正数，可知β越小则线段AP越短．(www.xing528.com)

在AL（即轴l）与平面M内任一直线所成的角中，最小的角是轴l与平面M所成的角，所以当点P位于轴l在平面M内的射影上，且∠ALP＝α时，线段AP是连接点A与截线Γ上任意一点的线段中最短的线段．

若轴l在平面M内的射影l0与圆锥面C一条母线的交点为B，且∠ALB＝α，则AB就是最短线段．

说明　在前面三个问题讨论中所取的基本量d，其实就是本问题中所说的“点A与截线Γ上任意一点的距离中的最小值”．

根据本问题讨论所得结论可知，如果平面M不经过圆锥面C［A；l，θ］的顶点A且与轴l斜交，它与圆锥面C的截线为Γ，那么连接点A与截线Γ上任意一点的线段中，最短的线段可如下确定：作轴l在平面M内的射影l0，设l0与l交于点L，在l0与圆锥面C的母线的交点中那个能使∠ALB＝α的点B，则线段AB就是最短线段．

注意，本问题研讨中没有包含轴l与平面M平行（即α＝0）的情况，这时的截线Γ是双曲线．

当轴l∥平面M时，设轴l在平面M内的射影为l0，直线l0与圆锥面C的两条母线分别交于点B1，B2，可知｜AB1｜＝｜AB2｜；如果分别过点B1，B2作垂直于轴l的平面，那么双曲线上的点位于所作的这两个平面外（除了点B1和B2），因此线段AB1和AB2是连接点A与截线Γ上任意一点的线段中的最短线段．

问题1-5　已知平面M与圆锥面C［A；l，θ］的截线Γ是椭圆，轴l在平面M内的射影l0与椭圆Γ相交于点A1，A2．那么，在连接椭圆Γ上任意两点的线段中，最长线段在什么位置？

分析　可联想椭圆的特征性质来进行讨论．

研讨　由椭圆的特征性质可知，椭圆Γ上任意一点到两个焦点F1，F2的距离之和等于定长m；还知焦点F1，F2位于轴l在平面M内的射影l0上，且在线段A1A2内．

如图1-21，设P，Q是椭圆Γ上任意两点，则

｜PF1｜＋｜PF2｜＝m，

｜QF1｜＋｜QF2｜＝m．

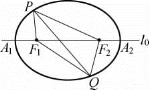
图1-21

∵｜PQ｜≤｜PF1｜＋｜QF1｜，当且仅当点P，Q，F1共线时等号成立；

｜PQ｜≤｜PF2｜＋｜QF2｜，当且仅当点P，Q，F2共线时等号成立，

∴2｜PQ｜≤｜PF1｜＋｜QF1｜＋｜PF2｜＋｜QF2｜＝2m，当且仅当点P，Q，F1，F2共线，即线段PQ经过点F1，F2时等号成立．

由于焦点F1，F2在线段A1A2内，而经过点F1，F2的直线只有一条，可知仅当线段PQ与线段A1A2重合时，得｜PQ｜＝｜A1A2｜＝m．

所以，连接椭圆Γ上任意两点的线段中，最长的线段是A1A2．

说明　根据对本问题研究所得的结论可知，线段A1A2是位于椭圆内部的最长的线段．结合问题1-3，得｜A1A2｜＝．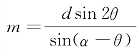

椭圆是平面M内的一条封闭曲线，因此位于椭圆内部的最长线段肯定存在．但是，双曲线在平面M内是无限延伸的，在连接双曲线上任意两点的线段中，显然没有最长的线段．注意到双曲线有两支，于是提出：

问题1-6　已知平面M与圆锥面C［A；l，θ］的截线Γ是双曲线，轴l在平面M内的射影l0与双曲线Γ相交于点A1，A2．那么，连接双曲线Γ上但不在同一支上的任意两点所得线段中，最短线段在什么位置？

分析　类比问题1-5，可联想双曲线的特征性质来进行讨论．

研讨　由双曲线的特征性质可知，双曲线Γ上任意一点到两个焦点F1，F2的距离之差的绝对值等于定长m；还知焦点F1，F2位于轴l在平面M内的射影l0上，且点A1，A2在线段F1F2内部．

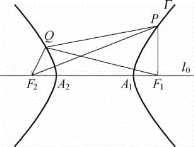
图1-22

设P，Q是双曲线Γ上但不在同一支上的任意两点．

（1）若点P位于Γ中内部含焦点F1的一支上，如图1-22所示，则点Q位于内部含焦点F2的一支上，得

｜PF2｜－｜PF1｜＝m，

｜QF1｜－｜QF2｜＝m．

∵｜PQ｜≥｜QF1｜－｜PF1｜，当且仅当点P，Q，F1共线时等号成立；

｜PQ｜≥｜PF2｜－｜QF2｜，当且仅当点P，Q，F2共线时等号成立，

∴2｜PQ｜≥｜QF1｜－｜PF1｜＋｜PF2｜－｜QF2｜＝｜PF2｜－｜PF1｜＋｜QF1｜－｜QF2｜＝2m，当且仅当点P，Q，F1，F2共线，即直线PQ经过点F1，F2时等号成立．

（2）若点P位于Γ中内部含焦点F2的一支上，则点Q位于内部含焦点F1的一支上，这时，

｜PF1｜－｜PF2｜＝m，｜QF2｜－｜QF1｜＝m．

与（1）同理，得2｜PQ｜≥2m，当且仅当点P，Q，F1，F2共线，即直线PQ经过点F1，F2时等号成立；此时线段PQ与线段A1A2重合，｜PQ｜＝｜A1A2｜＝m．

所以，连接双曲线Γ上但不在同一支上的任意两点所得线段中，最短线段是线段A1A2．

说明　根据对本问题研究所得的结论，可知线段A1A2是两端点分别位于双曲线一支上的线段中最短的线段．结合问题1-3，得．

容易看出，连接抛物线Γ上任意两点的线段中，不存在最长或最短的线段，不妨换一个角度提出研讨如下问题．

问题1-7　如果平面M与圆锥面C［A；l，θ］的截线Γ是抛物线，轴l在平面M内的射影为l0，其特征性质中的焦点为F、准线为l′，那么经过焦点F且两端点在抛物线Γ上的线段中，最短线段在什么位置？

分析　类同前面的研讨，可联想抛物线的特征性质．

研讨　由抛物线的特征性质可知，抛物线Γ上任意一点与焦点F的距离等于这点与准线l′的距离．

如图1-23所示，设线段PQ经过抛物线Γ的焦点F且端点P，Q在Γ上，分别作PT1⊥l′，QT2⊥l′，FT⊥l′，其中T1，T2，T分别是垂足，则

｜PQ｜＝｜PF｜＋｜QF｜＝｜PT1｜＋｜QT2｜≥2｜FT｜，当且仅当焦点F是线段PQ的中点时等号成立．

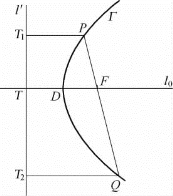
图1-23

由于“焦点F是线段PQ的中点⇔线段PQ垂直于l0”，因此经过点F且两端点在抛物线Γ上的线段中，最短线段是垂直于l0的线段，其长度为2｜FT｜．

说明　根据问题1-2研究所得的结论，可知｜FT｜＝｜DF｜＋｜DT｜＝2dsin2θ，所以经过焦点F且两端点在抛物线Γ上的线段中，最短线段是垂直于l0的线段，它的长度可用基本量θ，d表示为4dsin2θ．

在推导圆锥曲线的特征性质和统一性质的过程中，可见定长m、比值e是描述圆锥曲线特征性质的两个重要的量；再通过以上问题的研讨，还知椭圆、双曲线和抛物线中一些特殊线段的长度，都可用基本量θ，α，d来表示．

将以上研讨所得的结论归纳如下：

（1）对于比值e，可表示为e＝．当e＝1时，此圆锥曲线为抛物线．

（2）对于定长m：

如果m表示椭圆上任意一点与两个焦点的距离之和，那么

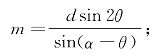
如果m表示双曲线上任意一点与两个焦点的距离之差的绝对值，那么

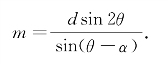
（3）讨论｜F1F2｜．

对于椭圆，由，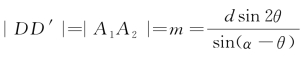

对于双曲线，由，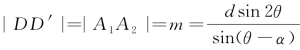

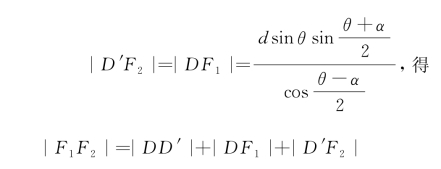
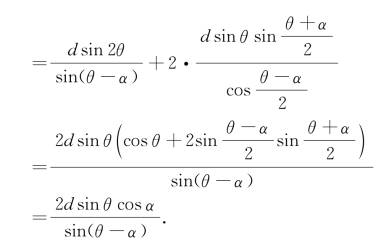
所以，椭圆两个焦点之间的距离为

双曲线两个焦点之间的距离为

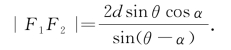
（4）讨论｜T1T2｜．

对于椭圆，由，

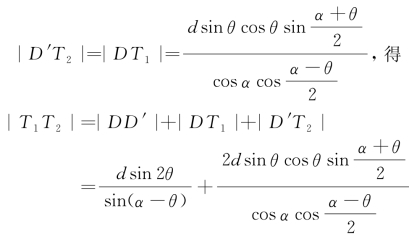
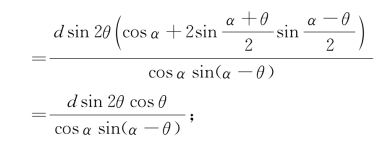
对于双曲线，由，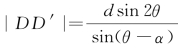

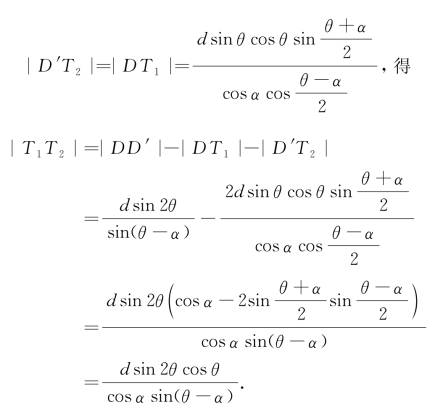
所以，椭圆两条准线之间的距离为

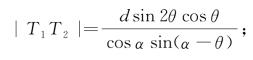
双曲线两条准线之间的距离为

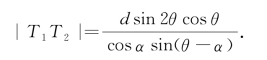
以上所讨论的数量e，m，｜F1F2｜，｜T1T2｜以及抛物线的焦点到准线的距离｜FT｜（可表示为｜FT｜＝2dsin2θ），它们统称为圆锥曲线的特征量．

（5）讨论｜F1F2｜，｜T1T2｜分别与e，m之间的关系．

对于椭圆，由

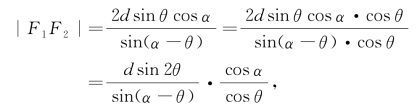
得｜F1F2｜＝me；

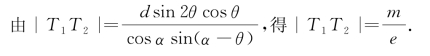
对于双曲线，同理可得｜F1F2｜＝me，．

进一步可知，对于椭圆和双曲线，都有｜F1F2｜＝e2｜T1T2｜．