圆锥曲线的统一性质探索

关于抛物线的特征性质，其推导是基于抛物线情形下只能作一个Dandelin球，其表述是“抛物线上任意一点与一个定点和一条定直线的距离相等”．而在椭圆、双曲线的特征性质的表述中，所列的等量关系涉及曲线上任意一点与两个定点的距离之“和”或“差”，有明显的共通之处．由此可见，抛物线的特征性质与椭圆、双曲线的特征性质在表述形式上的差别很大，并且可以肯定抛物线不会有类似于涉及两个定点的特征性质．

问题1-1　椭圆和双曲线是否也有类似于抛物线那样的特征性质？

分析　对于这个问题的探讨，一要考虑能否创设类似于研讨抛物线特征性质那样的情境；二要把握抛物线特征性质有关结论的实质，进而推测椭圆或双曲线的类似性质其结论可能是什么．

在截线呈现为椭圆或双曲线的圆锥面图形中，一定可作Dandelin双球，于是可选取其中一个球来创设情境．而抛物线特征性质的结论，可改述为“抛物线上任意一点与一个定点和一条定直线的距离之比的比值等于1”，于是可考虑将本问题改为：椭圆（或双曲线）上任意一点与一个定点和一条定直线的距离之比是否等于一个定值？

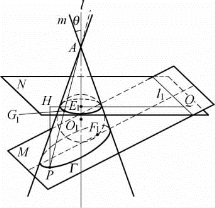
图1-13

研讨　设平面M与圆锥面C［A；l，θ］的截线Γ是椭圆或双曲线，轴l与平面M所成的角为α（α≠θ）．如图1-13所示，在圆锥面C内作一个Dandelin球O1，并设球O1与平面M的切点为F1，球O1与圆锥面C的切点圆为⊙E1，且⊙E1所在的平面为N，平面N与平面M的交线为l1．可知，轴l与平面N垂直．

设P是曲线Γ上任意一点，经过点P的母线AP与⊙E1交于点G1．连接PF1，可知｜PF1｜＝｜PG1｜．

在平面M内，过点P作PQ垂直于l1，点Q为垂足，可知｜PQ｜是点P到直线l1的距离．

再过点P作PH垂直于平面N，点H为垂足．由直线PH与轴l同垂直于平面N，可知直线PH与轴l平行．已知轴l与圆锥面C的母线的夹角为θ，轴l与平面M所成的角为α，可知PH与圆锥面C的母线的夹角为θ，PH与平面M所成的角为α．另外，还可知PH在平面M内的射影是PQ．

在Rt△P H G1和Rt△P H Q中，∠G1P H＝θ，∠QPH＝α，得(www.xing528.com)

因为α和θ都是定角，所以是一个定值．

当θ＜α＜时，截线Γ是椭圆，这时cosθ＞cosα＞0，可知0＜e＜1；

当0≤α＜θ＜时，截线Γ是双曲线，这时0＜cosθ＜cosα，可知e＞1．综上所述，得

（1）椭圆上任意一点与定点F和定直线l′的距离之比等于定值e，且0＜e＜1；

（2）双曲线上任意一点与定点F和定直线l′的距离之比等于定值e，且e＞1．

上述关于椭圆和双曲线性质的真命题（1）（2），其逆命题也正确．

将命题（1）（2）分别表述为椭圆和双曲线的特征性质，再与抛物线的特征性质一起归纳，就得到圆锥曲线的统一的特征性质，简称为圆锥曲线的统一性质．圆锥曲线的统一性质表述如下：

圆锥曲线是平面内与一个定点和一条定直线的距离之比等于定值e的点所成的集合．当0＜e＜1时，它是椭圆；当e＞1时，它是双曲线；当e＝1时，它是抛物线．

说明　在本问题研究所得的圆锥曲线的统一性质中，所涉及的那个定点称为焦点，那条定直线则称为准线．易知，一个椭圆一定有两个焦点和两条准线，其中的一个焦点与一条准线相互对应；双曲线也是如此．对于一条抛物线，它只有一个焦点和一条准线．