圆锥曲线的特征性质优化

为使表述简洁些，以下将“顶点为A、母线与轴l的夹角为θ的圆锥面C”简记为“圆锥面C［A；l，θ］”．另外，在此指明“性质p是点集Γ的特征性质”就是“P∈Γ⇔点P具有性质p”．

下面，我们主要运用几何推理的方法对圆锥曲线的特征性质进行研讨．

（1）椭圆的特征性质　设圆锥面C［A；l，θ］，平面M不经过点A，轴l与平面M所成的角为α，且θ＜α＜，则平面M与圆锥面C的截线Γ是一个椭圆，如图1-5所示．

图1-5

怎样探究椭圆的特征性质？前面的例1和例2给予我们有益的启示．

思考1　利用Dandelin双球来描述平面M与圆锥面C的相对位置．

给定平面M，即平面M的位置是确定的，则与圆锥面C和平面M都相切的球也完全确定．根据例1的讨论可知，在θ＜α＜的条件下，与圆锥面C及平面M都相切的球有两个，它们位于平面M的两侧又同在圆锥面C的一支内．这两个球的确定性，是平面M与圆锥面C的相对位置的反映．

图1-6

在图1-5中，在平面M的两侧分别作球O1和球O2，使球O1、球O2都与圆锥面C及平面M分别相切．设球O1、球O2与平面M的切点分别为F1和F2，这两个球与圆锥面C的切点圆分别为⊙E1和⊙E2；再设⊙E1所在的平面为N1，⊙E2所在的平面为N2，如图1-6所示．

思考2　椭圆Γ上的点都在所作的球外，可知从Γ上一点引球的切线，所得的切线长相等．于是，可建立有关线段长度的相等关系．

设P是椭圆Γ上任意一点，过点P的母线AP与⊙E1和⊙E2分别相交于点G1和G2．连接PF1，则线段PF1与PG1是从球O1外一点P向球O1所引的两条切线段，所以｜PF1｜＝｜PG1｜．连接PF2，同理，可得｜PF2｜＝｜PG2｜．

∴｜PF1｜＋｜PF2｜＝｜PG1｜＋｜PG2｜＝｜G1G2｜．

思考3　由线段G1G2所处位置的特征，可判断它的长度是一个定值．

根据球与圆锥面相切所得切点圆的性质，可知平面N1、平面N2都与轴l垂直．对于椭圆上的一点P，如上所作的线段G1G2在母线AP上且夹在同垂直于轴l的两个平面N1与N2之间．由圆锥面C具有旋转变换的保长性可知，位于圆锥面C母线上且夹在平面N1和平面N2之间的所有线段等长．所以，相应于椭圆Γ上任意一点P的｜G1G2｜是一个定值．

思考4　明确椭圆Γ上的点的特性．

记｜G1G2｜为m，可得椭圆Γ上任意一点P与F1，F2两点的距离之和等于定值m，其中F1，F2是平面M分别与球O1和球O2相切的切点，这是两个定点．所以，椭圆Γ上任意一点与两个定点F1，F2的距离之和等于定值m．

由｜PF1｜＋｜PF2｜＝｜G1G2｜和｜PF1｜＋｜PF2｜＞｜F1F2｜，可知m＞｜F1F2｜．

思考5　如果平面M上一点K满足条件｜KF1｜＋｜KF2｜＝m，推断点K应在椭圆Γ上．

已知点K在平面M上且满足条件｜KF1｜＋｜KF2｜＝m，假设点K不在椭圆Γ上．

因为椭圆Γ以及点K，F1和F2都在平面M内，而且点F1和F2在椭圆Γ内部，所以线段F1K或其延长线必与椭圆Γ交于一点R，可得点K在线段F1R的延长线上或者在线段F1R上．因为点R在椭圆Γ上，所以｜RF1｜＋｜RF2｜＝m．

在平面M上，如图1-7所示（图中点K′表示点K位于线段F1R上），可知

图1-7

｜KF1｜＋｜KF2｜＝｜RF1｜＋（｜KR｜＋｜KF2｜）＞｜RF1｜＋｜RF2｜

（或｜K′F1｜＋｜K′F2｜＝｜RF1｜－｜K′R｜＋｜K′F2｜＜｜RF1｜＋｜RF2｜）．

于是，得｜KF1｜＋｜KF2｜≠m，这与已知｜KF1｜＋｜KF2｜＝m相矛盾，所以点K一定在椭圆Γ上．

这就是说，在平面M内与两个定点F1，F2的距离之和等于定值m的点在椭圆Γ上．

思考6　概括椭圆的特征性质．

综上所述，可知椭圆具有如下特征性质：在平面内，

一个点在椭圆上⇔这个点与两个定点的距离之和等于定值．

椭圆的这一特征性质也可表述为：

椭圆是平面内与两个定点的距离之和等于定值的点所成的集合，其中的定值大于这两个定点的距离．

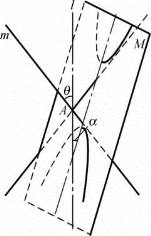
图1-8

（2）双曲线的特征性质　设圆锥面C［A；l，θ］，平面M不经过点A，轴l与平面M所成的角为α，且0≤α＜θ，则平面M与圆锥面C的截线Γ是双曲线，如图1-8所示．

思考1　同推导椭圆的特征性质那样，利用Dandelin双球来描述平面M与圆锥面C的相对位置．

在0≤α＜θ的条件下，与圆锥面C及平面M都相切的球也有两个，这两个球同在平面M的一侧，但分别位于圆锥面的两支内．

在图1-8中，分别在圆锥面C的两支内作球O1和球O2，使球O1、球O2分别都与圆锥面C及平面M相切，如图1-9所示．

图1-9

思考2　类似于探讨椭圆特征性质那样，对双曲线的特征性质进行探讨．(www.xing528.com)

同样设切点F1，F2，并设切点圆⊙E1和⊙E2，两切点圆所在的平面分别为N1和N2，仍有平面N1与平面N2都垂直于轴l．

设P是双曲线Γ上任意一点，经过点P的母线AP与⊙E1和⊙E2的交点分别为G1和G2．

注意到切点F1和F2的位置、切点圆⊙E1和⊙E2的位置，以及它们的位置情况与椭圆情形的差别，得到有关线段的长度关系是：

当｜PF1｜＞｜PF2｜时，｜PF1｜－｜PF2｜＝｜PG1｜－｜PG2｜＝｜G1G2｜；

当｜PF1｜＜｜PF2｜时，｜PF2｜－｜PF1｜＝｜PG2｜－｜PG1｜＝｜G1G2｜，

即｜｜PF1｜－｜PF2｜｜＝｜G1G2｜．

由圆锥面C是旋转面可知，相应于双曲线上任意一点P的｜G1G2｜是一个定值，记作m．又由｜｜PF1｜－｜PF2｜｜＝｜G1G2｜和｜｜PF1｜－｜PF2｜｜＜｜F1F2｜，可知0＜m＜｜F1F2｜．

思考3　概括双曲线的特征性质．

通过以上讨论，得

双曲线Γ上任意一点与两个定点F1，F2的距离之差的绝对值等于定值m．

反过来，如果点K在平面M内，｜｜KF1｜－｜KF2｜｜＝m（其中0＜m＜｜F1F2｜），那么同前面研讨椭圆的情形一样，可证明点K在双曲线Γ上．

所以，双曲线具有如下特征性质：在平面内，

一个点在双曲线上⇔这个点与两个定点的距离之差的绝对值等于定值．

双曲线的这一特征性质也可表述为：

双曲线是平面内与两个定点的距离之差的绝对值等于定值的点所成的集合，其中的定值小于这两个定点的距离．

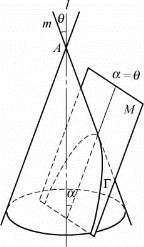
图1-10

（3）抛物线的特征性质　设圆锥面C［A；l，θ］，平面M不经过点A，轴l与平面M所成的角为α，且α＝θ，则平面M与圆锥面C的截线Γ是抛物线，如图1-10所示．

思考1　利用Dandelin球来描述平面M与圆锥面C的相对位置．

在α＝θ的条件下，可作且只能作一个球与圆锥面C及平面M都相切．这个球的确定性虽然也是平面M与圆锥面C的相对位置的反映，只是这时仅有一球，与前面（1）（2）出现Dandelin双球的情境有所不同，所以要寻找新的路径来探讨抛物线的特征性质．

对于平面M进行定位时，这个球与平面M的切点，以及它与圆锥面C的切点圆，都有重要的参照作用；还有如切点圆所在平面与平面M相交的情况等也可用作参照．可从中选择路径，建立有用的几何关系．

思考2　再借助于Dandelin球与圆锥面C的切点圆所在的平面来探讨．

在图1-10中作球O，使它与圆锥面C和平面M都相切，如图1-11所示．

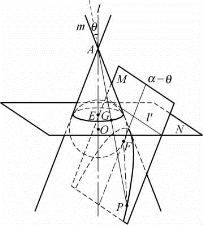
图1-11

设球O与平面M的切点为F，球O与圆锥面C的切点圆为⊙E，⊙E所在的平面记为N，平面N与平面M的交线为l′．可知，轴l与平面N垂直，l′是定直线．

图1-12

设P是抛物线Γ上任意一点，过点P的母线AP与⊙E相交于点G．连接PF，可知线段PF和PG是经过球O外一点P的切线段，得｜PF｜＝｜PG｜．

思考3　寻找与线段PG长度相等的线段．

如图1-12所示，过点P作PH垂直于平面N，点H为垂足．再在平面N内作HQ垂直于直线l′，点Q为垂足．连接PQ，可知PQ⊥l′．注意到相交直线PH和PQ都与l′垂直，可知l′与由PH和PQ所确定的平面PHQ垂直，则经过直线l′的平面M与平面PHQ垂直．于是，平面PHQ与平面M的交线PQ就是直线PH在平面M内的射影．

由直线PH与轴l同垂直于平面N，可知直线PH与轴l平行．已知轴l与圆锥面C的母线的夹角为θ，与平面M所成的角也为θ，可知直线PH与圆锥面C的母线的夹角以及与平面M所成的角同为θ．

在Rt△PHG和Rt△PHQ中，∠GPH＝∠QPH＝θ，得｜PG｜＝｜PQ｜．

思考4　联想｜PQ｜的几何意义，概括抛物线上的特征性质．

因为PQ⊥l′，点Q为垂足，所以｜PQ｜是点P到直线l′的距离．

由｜PF｜＝｜PG｜，｜PG｜＝｜PQ｜，得｜PF｜＝｜PQ｜．

通过以上讨论，得

抛物线上任意一点与定点F的距离等于这点与定直线l′的距离．

反过来，如果点K在平面M内，点K与点F的距离等于点K到直线l′的距离，那么也可以证明点K一定在抛物线Γ上．

所以，抛物线具有如下特征性质：在平面内，

一个点在抛物线上⇔这个点与一个定点和一条定直线的距离相等．

抛物线的这一特征性质也可表述为：

抛物线是平面内与一个定点和一条定直线的距离相等的点所成的集合，其中的定点在这条定直线外．