圆锥曲线的定义及截线形态与截平面位置的关系

一个平面与圆锥面相交，也可以说是“用一个平面去截圆锥面”，这个平面就称为截平面，它们的交线又称为截线．

用一个平面去截一个圆锥面，所得截线的形态与截平面的位置有关．

设圆锥面C的顶点为A，母线与轴l的夹角为θ；轴l与平面M所成的角为α，0≤α≤．

（1）如果平面M经过顶点A，那么平面M与圆锥面C的截线Γ有三种可能的情况：

当θ＜α≤时，截线Γ只含有一个点A；

当α＝θ时，截线Γ是一条母线；

当0≤α＜θ时，截线Γ是两条母线．

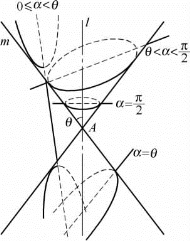
（2）如果平面M不经过顶点A，那么平面M与圆锥面C的截线Γ有四种可能的情况，如图1-2所示：

(www.xing528.com)

图1-2

当α＝时，截线Γ是一个圆；

当θ＜α＜时，截线Γ称为椭圆；

当α＝θ时，截线Γ称为抛物线；

当0≤α＜θ时，截线Γ称为双曲线．

由（2）中四种情况所得的截线，统称为圆锥曲线，它们其实都是平面M内的曲线．由（1）中三种情况所得的截线，则称为退化的圆锥曲线．

对于（2）中当时截线Γ是一个圆，说理如下：设轴l与平面M垂直于点E，则E是顶点A在平面M内的射影．由旋转变换的保长性可知，位于圆锥面母线上且夹在点A与平面M间的所有线段等长，则这些线段在平面M内的射影也等长，所以点E到截线Γ上各点的距离相等，Γ是以点E为圆心的一个圆．

截线Γ是圆的这种情况在此不作深入研究，后面所说的圆锥曲线主要是指椭圆、抛物线和双曲线．由于（2）中当θ≤α＜时，平面M只与圆锥面C的一支相交，可知椭圆、抛物线只与圆锥面C的一支有关；而当0≤α＜θ时，平面M一定与圆锥面C的两支都相交，所以双曲线有两支．