探索性因子分析研究及优化方法

本研究将收集的173套有效问卷随机分成两份，分别用来进行探索性因子分析（87套问卷）和验证性因子分析（86套问卷）。探索性因子分析的原理是通过主成分分析法，即对每一个概念进行因素抽取，并采用正交旋转的方差最大法来进行验证，最终确定测量条目的因子载荷。

对87套问卷数据进行探索性因子分析前，先对其进行了共同构面的一致性检验，包括共同度检验以及校正题项的总相关度检验（corrected item-total correlation，CITC），其临界参考值分别为0.3和0.4。如果有题项的CITC小于0.3，则说明该题项与整体量表的同质性比较低，需要对该题项予以删除；同理，如果结果显示有题项的CITC小于0.4，则说明该题项与其他题项的相关性较低，因此需要对其进行删除。基于上述两个标准，我们对计划做EFA分析（探索性因子分析）的数据进行了检验，总共删除1个题项，即第13题“公司给我提供的工作让我觉得有意义”。

然后，对剩余的12个题项进行KMO与Barlett球形检验。KMO与Bartlett球形检验指标可以说明测量指标的效度。当KMO超过其临界值0.7，Bartlett球形检验超过其临界值0.05的显著水平时，表明比较适合用探索性因子分析。统计结果显示，KMO值为0.862，Barlett球形检验结果显著（近似卡方χ2=745.092，df=66，在0.001水平上显著），说明接下去的探索性因子分析法有效。在此基础上，我们采用主成分分析法进行探索性因子分析，获得最大方差旋转后的成分矩阵。遵循对单个维度上载荷系数得分都超过0.5（即跨维度），或者所有维度上载荷系数得分都没有超过0.5的题项予以删除的原则，又删除了3个题项，删除项第4题“公司重视员工对公司整体政策的反馈”、第6题“公司关心员工的工作满意度”、第8题“公司重视员工的工作建议”。

经过上述两个步骤的修订和完善，一共删除了4个题项，接下去再对剩余的9个题项进行因子分析，其KMO值为0.798，Bartlett球形检验的结果显著（近似卡方值即χ2=447.290，df=28，并且在0.001的水平上显著），证明适合进行因子分析。然后通过主成分分析法，选择特征值大于1，最大方差旋转后析出两个清晰的因子，累计的方差解释度达到73.595%，其探索性因子分析结果如表5-12所示。

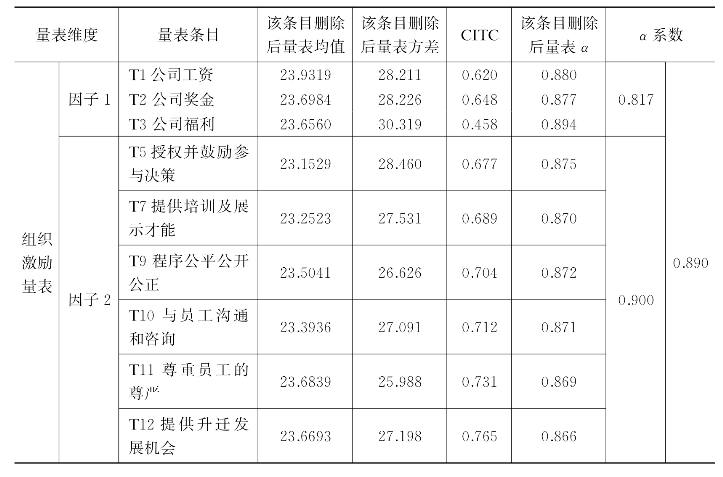
最后，研究采用信度和效度的方法来对删除后的测试条目进行评估，结果如表5-13所示。本研究采用Cronbach'sα信度系数来验证测量变量的效度，最终确定测量变量的条目。α信度系数检验采用大于0.7的标准，表明内在一致性较好，符合信度的要求。(www.xing528.com)

表5-12　量表探索性因子分析结果

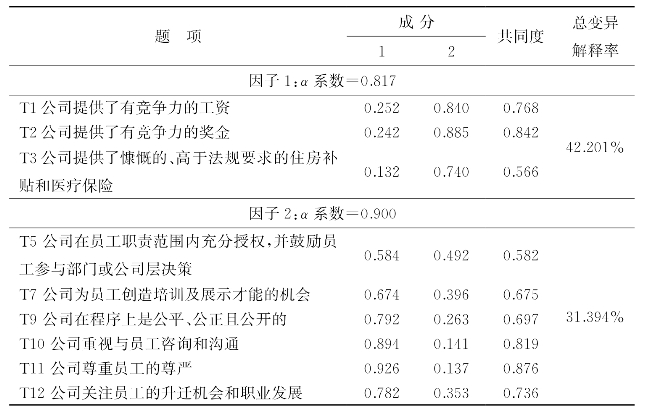
表5-13　新开发量表信度分析结果

在进行上述操作后，得到了组织激励的修订量表，它包含两个维度：①因子1包括了员工薪酬的竞争性和福利水平，其测量表达了组织在制定组织激励时考虑的满足员工物质方面的需求，因此，笔者将因子1命名为“组织物质激励”，其α系数为0.817，一致性程度较高；②因子2主要测量的是组织对员工工作的保障，对员工的尊重、关心，它体现了组织对员工长期发展的考虑，因此笔者将因子2命名为“组织发展激励”，其α系数为0.900，一致性程度非常好。我们对组织激励量表的探索性因子分析的结果表明，数据基本上符合研究对组织激励二维度构思的想法。