如何进行员工能力低时的数值分析以优化绩效

员工能力低时，根据假设此时θij＝1，员工努力程度的均衡解(7.17)和(7.23)式中只剩下变量γi，为了计算过程的简便，此处取20＞γ1＞γ2＞0范围内的整数进行数值分析。题中的变量取值见表7.6。

图7.1　员工能力高时，员工努力程度与公平偏好系数、能力系数的关系图

注:图7.1中的四条线分别表示4名员工不同能力系数和公平偏好下的努力程度。

图7.2　员工能力高时，同质组合与异质组合企业总收益对比图

注:虚线表示同质量组合企业总收益，实线表示异质组合企业总收益。

表7.6　员工能力低时变量γi的取值

(www.xing528.com)

依据员工能力低时的均衡解aij＝1+γi，i＝1，2。结合表7.6变量的取值可以得出相应的员工努力程度和企业总收益(见表7.7)。

表7.7　员工的努力程度和企业总收益

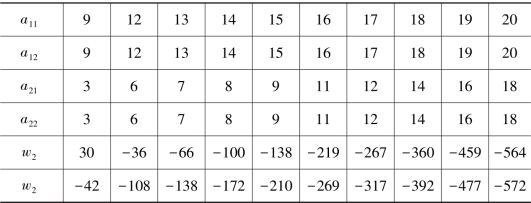
将表7.7中的数值代入员工能力低时员工组合的均衡解(7.17)和(7.23)式中，运用MATLAB软件可以画出该表中员工的努力程度与公平偏好系数的关系图7.3，将赋值的变量代入员工的企业总收益(7.18)、(7.24)式中，运用MATLAB软件做出同质组合和异质组合企业总收益的对比图7.4。如图7.3所示，员工的公平偏好系数与员工努力程度的关系是线性的，且是单调递增的关系，当员工的能力较低时，员工能力系数为1，员工的努力程度随着员工公平偏好系数的增大而增大，这也与7.5.1中数值分析的结果吻合。如图7.4所示，可以看出系列1蓝线也就是异质组合的企业总收益总在系列2红线同质组合总收益的上面，也就是员工能力低时，异质组合的企业总收益要大于同质组合的总收益，此时，异质组合方式为企业员工的最佳组合方式。

图7.3　员工能力低时员工努力程度与公平偏好系数的关系图

图7.4　员工能力低时，同质和异质组合企业总收益对比图

注:虚线表示异质组合企业总收益，实线表示同质组合企业总收益。