稳定匹配模型构建方法：一对多

依据简化后的偏好列表G′（Ai）和G′（Bj），以及Bj在偏好列表P（Ai）中的序值rA（i，j）和Ai在偏好列表P（Bj）中的序值rB（i，j），在考虑匹配稳定性的条件下，可以构建以甲方主体满意度最大和乙方主体满意度最大为目标的双目标优化模型。设xij为0-1型决策变量，xij=1表示第i个甲方主体与第j个乙方主体匹配；否则xij=0。本章构建的双目标优化模型（7.1a）—（7.1f）如下：

在模型（7.1a）—（7.1f）中，式（7.1a）和（7.1b）为目标函数，其中，式（7.1a）表示最小化甲方主体的序值之和，式（7.1b）表示最小化乙方主体的序值之和；式（7.1c）—（7.1f）为约束条件，其中，式（7.1c）为匹配数量约束条件，表示每个甲方主体最多与一个乙方主体进行匹配；式（7.1d）为匹配数量约束条件，表示每个乙方主体Bj最多可以与qj个甲方主体进行匹配；式（7.1e）为根据文献[392]的思想确定的一对多双边匹配的稳定性约束条件。

为了说明所建立模型（7.1a）—（7.1f）的合理性，下面对如下的定理7.1进行证明。

定理7.1 在一对多双边匹配问题中，满足约束条件（7.1e）的匹配方案是一个稳定匹配，该条件称为一对多双边匹配的稳定性约束条件。(www.xing528.com)

证明：为了证明约束条件（7.1e）能够保证获得的匹配方案是一对多双边匹配的稳定匹配，可以证明G′（Ai）和G′（Bj）中的Ai和Bj不会个体阻塞匹配方案，同时（Ai，Bj）不会成对阻塞匹配方案。通过偏好列表简化规则步骤4可知，G′（Ai）和G′（Bj）中的（Ai，Bj）都是可接受对，因此由性质7.1可知，对于G′（Ai）和G′（Bj）中的Ai和Bj不会个体阻塞匹配方案。为了证明满足约束条件（7.1e）的可接受对（Ai，Bj）不会成对阻塞匹配方案，可以证明若（Ai，Bj）满足式（7.2），则（Ai，Bj）一定是阻塞对。

由于xij∈{0，1}，若保证式（7.2）成立，则一定有，且。由可知，对于Ai有μ（Ai）=Ai或者μ（Ai）=Bh，；而由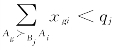可知，对于Bj有|μ（Bj）|＜qj或。此外，由于xij=0，那么由成对阻塞的定义7.3可知，此时（Ai，Bj）一定是阻塞对。因此，若可接受对（Ai，Bj）满足约束条件（7.1e），则（Ai，Bj）一定不是阻塞对。

综上可知，式（7.1e）能够保证获得的匹配方案是一对多双边匹配的一个稳定匹配方案。