相关概念及个体阻塞在一对多双边匹配中的性质

在文献[2]的基础上，本章对基于偏好序信息的一对多双边匹配问题中的可接受对、个体阻塞、成对阻塞、稳定匹配等概念进行界定。

定义7.1（可接受对） 在一对多双边匹配问题中，对于∀Ai∈A，∀Bj∈B，若Bj∈P（Ai）且Ai∈P（Bi），则称（Ai，Bj）为可接受对；否则，称为不可接受对。

在匹配方案μ中，若存在一个匹配主体的匹配对象对该匹配主体而言是不可接受的，则称匹配方案μ被该匹配主体个体阻塞。

定义7.2（个体阻塞） 设一对多双边匹配μ：A∪B→2A∪B，若存在Ai∈A，Bj∈B，满足以下两种情况之一：

（1）μ（Ai）≠Ai，且Ai≻Aiμ（Ai）；

（2）Ai∈μ（Bj），且Bj≻BjAi，

则称一对多双边匹配μ被个体阻塞。

定义7.3（成对阻塞） 设一对多双边匹配μ：A∪B→2A∪B，对于∀Ai∈A，∀Bj∈B，若可接受对（Ai，Bj）满足以下条件之一：

(1)μ(Ai)=Ai,|μ(Bj)|＜qj;

（2）μ（Ai）=Ai，且∃Ag∈μ（Bj）qj，Ai≻BjAg；

（3）μ（Ai）=Bh，|μ（Bj）|＜qj，且Bj≻AiBh；

（4）μ（Ai）=Bh，∃Ag∈μ（Bj），且Bj≻AiBh，Ai≻BjAg。

则称一对多双边匹配μ被（Ai，Bj）成对阻塞，并称（Ai，Bj）为匹配方案μ的一个阻塞对。(www.xing528.com)

定义7.4（一对多稳定匹配） 设一对多双边匹配μ：A∪B→2A∪B，若匹配方案μ既不被任何个体阻塞，并且也不被任何可接受对成对阻塞，则称μ为稳定匹配；否则，称μ为不稳定匹配。

由定义7.1—定义7.4容易获得以下性质：

性质7.1 若匹配方案μ的所有匹配对都是可接受对，则匹配方案μ不会被个体阻塞。

性质7.2 在匹配方案μ中，若不可接受对（Ai，Bj）是匹配方案μ的一个匹配对，则μ一定是不稳定匹配，即稳定匹配中的所有匹配对都是可接受对。

性质7.3 不可接受对一定不是匹配方案的阻塞对。

依据文献[2]和文献[325]，下面分别给出甲方主体最优稳定匹配和乙方主体最优稳定匹配的数学定义。

定义7.5（甲方主体最优稳定匹配） 在一对多双边匹配问题（A，B；P）中，设Us表示由匹配主体集合A、B以及偏好列表集合P确定的所有一对多稳定匹配的集合，记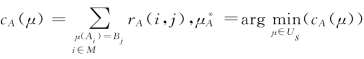，），则称为甲方主体最优稳定匹配。

依据文献[2]和定义7.5、定义7.6，可以获得如下性质：

性质7.4 在一对多双边匹配问题（A，B；P）中，设U s表示由匹配主体集合A、B以及偏好列表集合P确定的所有一对多稳定匹配的集合，对于∀μ∈U s，令}，则有；类似地，有。

由性质7.4可知，在甲方主体最优稳定匹配中，甲方主体的匹配对象是所有稳定匹配中最优的，而乙方主体获得的最差匹配对象也是所有稳定匹配中最差的；类似地，在乙方主体最优稳定匹配中，甲方主体的匹配对象是所有稳定匹配中最差的，而乙方主体获得的最好匹配对象也是所有稳定匹配中最好的。

本章要解决的问题是：依据甲方主体Ai给出的偏好列表P（Ai）与乙方主体Bj给出的偏好列表P（Bi），通过有效的双边匹配方法，获得双边匹配主体满意度尽可能大的一对多双边稳定匹配方案。