优化模型构建与求解的方法和技巧

在家政服务人员与雇主的双边匹配过程中，满意度是衡量匹配方案优劣的一个重要准则。家政服务人员对雇主越满意，则家政服务人员越愿意为雇主提供家政服务；类似地，雇主对家政服务人员越满意，雇主越愿意雇佣家政服务人员。为了获得家政服务人员与雇主满意度尽可能高的技能约束稳定匹配，首先给出家政服务人员Wi对雇主Ej的满意度αij和雇主Ej对家政服务人员Wi的满意度βij的计算公式；然后构建以家政服务人员与雇主总体满意度最大为目标的优化模型，并证明模型中线性约束条件构成的解空间对应的匹配方案与HSM（1，1，n，1）问题的技能约束稳定匹配是一一对应的；最后采用ε-constraint算法对双目标优化模型进行求解。

（1）满意度计算

在现实的家政服务人员与雇主双边匹配过程中，家政服务人员由于个人心理行为的影响，使得对雇主的满意度与偏好排序值之间往往呈现非线性的关系，例如，对排在第1位的雇主满意度可能为1，对第2位的雇主满意度为0.95，对第3位的雇主满意度为0.82，等等。类似地，雇主对家政服务人员的满意度与偏好排序值之间也存在这种非线性关系。因此，为了更准确地刻画家政服务人员和雇主的满意度，本书采用如下公式（6.5）来计算家政服务人员对雇主的满意度。

其中，M为足够大的正数。

本书采用如下公式（6.6）来计算雇主对家政服务人员的满意度。

在式（6.5）和（6.6）中，家政服务人员和雇主的满意度是关于序值的严格单调递减函数。当家政服务人员Wi认为雇主Ej是可接受的时，0≤αij＜1。特别地，当Wi认为n个雇主都是可接受的，并且Wi把Ej排在最后一位，即rij=n时，αij=0；当家政服务人员Wi认为雇主Ej是不可接受的时，αij=-M。雇主对家政服务人员的满意度也具有上述类似的性质。

（2）模型构建

依据上述得到的家政服务人员满意度αij和雇主满意度βij，可以建立家政服务人员和雇主总体满意度最大为目标的优化模型。设xij为0-1型决策变量，xij=1表示家政服务人员Wi与雇主Ej形成匹配对；否则，xij=0。进一步地，可构建如下的0-1型双目标整数规划模型（6.7a）—（6.7i）。

在模型（6.7a）—（6.7i）中，式（6.7a）和（6.7b）为目标函数，式（6.7a）表示最大化家政服务人员的满意度，式（6.7b）表示最大化雇主的满意度。式（6.7c）—（6.7i）为约束条件，其中，式（6.7c）和（6.7d）为匹配数量约束，式（6.7c）表示一个雇主最多需要一个家政服务人员，式（6.7d）表示一个家政服务人员最多为一个雇主提供服务；式（6.7e）为偏好可接受对约束，能够保证进行匹配的家政服务人员与雇主是偏好可接受的；式（6.7e）为技能可接受对约束，能够保证家政服务人员与雇主进行匹配时需要满足服务技能约束；式（6.7g）为技能约束稳定匹配的约束条件，其中M是一个足够大的正数。

对于任意的HSM（1，1，n，1）问题，设由模型（6.7a）—（6.7i）的可行解构成的稳定匹配集合为Ω，HSM（1，1，n，1）的所有稳定匹配构成的集合为U。

引理6.1 模型（6.7a）—（6.7i）的任意一个可行解对应的匹配方案都是HSM（1，1，n，1）问题的一个技能约束稳定匹配，Ω=U。

证明：设模型（6.7a）—（6.7i）的任意一个可行解为X=[xij]m×n，i∈{1，2，…，m}，j∈{1，2，…，n}，与可行解X对应的匹配方案为μ。约束条件（6.7c）和（6.7d）作为匹配数量约束，保证了家政服务人员与雇主的一对一双边匹配，即家政服务人员最多与一个雇主匹配，一个雇主最多与一个家政服务人员匹配。因此，μ是HSM（1，1，n，1）问题的一个一对一双边匹配。（6.7e）和（6.7f）分别是偏好可接受对约束和技能可接受对约束，保证了μ是可行技能约束匹配。

为了证明式（6.7g）能够保证可行技能约束匹配μ是技能约束稳定匹配，可以证明满足式（6.7g）的∀Wi∈W和∀Ej∈E组成的（Wi，Ej）不是技能约束阻塞对。若（Wi，Ej）是一个偏好不可接受对，即σij=1时，式（6.7g）一定成立，显然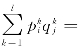此时（Wi，Ej）不是技能约束阻塞对。若（Wi，Ej）是技能不可接受对，即0，则式（6.7g）一定成立，显然此时（Wi，Ej）不是技能约束阻塞对。下面证明若（Wi，Ej）是偏好可接受对和技能可接受对，则约束条件（6.7g）能够保证（Wi，Ej）不是一个技能约束阻塞对。

若（Wi，Ej）是偏好可接受对，即σij=0，则（6.7g）化简为式（6.8）。

而又由于（Wi，Ej）是技能可接受对，即，因此，式（6.8）可化简为

为了证明满足式（6.9）的偏好可接受对和技能可接受对（Wi，Ej）不是技能约束阻塞对，可证明若（Wi，Ej）满足式（6.10），则（Wi，Ej）一定是技能约束阻塞对。

式（6.10）可进一步化简为

由于xij∈{0，1}，所以由式（6.11）可得。由此可知，对于Wi有μ（Wi）=Wi或μ（Wi）=Eh，rij＜rih；而对于Ej有μ（Ej）=Ej或μ（Ej）=Wk，tij＜tkj。那么由技能约束稳定匹配的定义6.8可知，偏好可接受对和技能可接受对（Wi，Ej）一定是技能约束阻塞对。因此，约束条件（6.7g）能够保证获得的可行技能约束匹配是技能约束稳定匹配。由此可证，模型（6.7a）—（6.7i）的任意一个可行解都是HSM（1，1，n，1）问题的一个技能约束稳定匹配，即Ω⊆U。证毕

引理6.2 HSM（1，1，n，1）问题的任意一个技能约束稳定匹配都是模型（6.7a）—（6.7i）的一个可行解，即U⊆Ω。

证明：设μ是HSM（1，1，n，1）问题的一个技能约束稳定匹配方案。对于∀Wi∈W，∀Ej∈E，若（Wi，Ej）∈μ，则令xij=1；否则，xij=0。由于μ是一个一对一双边匹配，Wi和Ej没有匹配对象或最多有一个匹配对象，因此，匹配数量约束（6.7c）和（6.7d）成立。此外，由定义6.5和引理6.2可知，μ中的匹配对都是偏好可接受对和技能可接受对，因此，约束条件（6.7e）和（6.7f）一定成立。下面证明技能约束稳定匹配μ对应的模型解满足约束条件（6.7g）。在技能约束稳定匹配μ中，若Wi和Ej形成了匹配对，即xij=1时，由于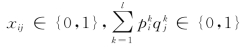，σij∈{0，1}且M是一个足够大的正数，那么显然约束条件（6.7g）是成立的。在Wi和Ej没有形成匹配对，即xij=0的情形下，若（Wi，Ej）是偏好不可接受对，此时σij=1，那么显然约束条件（6.7g）是成立的；若（Wi，Ej）是技能不可接受对，即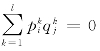时，此时约束条件（6.7g）是成立的。在xij=0且（Wi，Ej）是偏好可接受对和技能可接受对的情形下，为了证明当（Wi，Ej）不是匹配方案μ的技能约束阻塞对时，约束条件（6.7g）一定成立，可证若（Wi，Ej）是技能约束阻塞对，则约束条件（6.7g）一定不成立。由于（Wi，Ej）是偏好可接受对，则有M=0；由于（Wi，Ej）是技能可接受对，则有，此外由于xij=0，因此，此时约束条件（6.7g）化简为

依据定义6.7，分以下几种情况进行讨论：

（i）μ（Wi）=Eh，rij＜rih，μ（Ej）=Wk，tij＜tkj。由于μ（Wi）=Eh，rij＜rih，则；由于μ（Ej）=Wk，tij＜tkj，则。显然，此时式（6.12）不成立。

（ii）μ（Wi）=Eh，rij＜rih，μ（Ej）=Ej。由于由于μ（Ej）=Ej，即Ej没有实现匹配，则。显然，此时式（6.12）不成立。(www.xing528.com)

（iii）μ（Wi）=Wi，μ（Ej）=Wk，tij＜tkj。由于μ（Wi）=Wi，即Wi没有实现匹配，则；由于μ（Ej）=Wk，tij＜tkj，则。显然，此时式（6.12）不成立。

（iv）μ（Wi）=Wi，μ（Ej）=Ej。由于μ（Wi）=Wi，μ（Ej）=Ej，则。显然，此时式（6.12）不成立。

由此可知，在xij=0且（Wi，Ej）是偏好可接受对和技能可接受对情形下，若（Wi，Ej）不是匹配方案μ的技能约束阻塞对，约束条件（6.7g）一定成立。由此可证，在技能约束匹配方案μ中，∀Wi∈W，∀Ej∈E都能使得约束条件（6.7g）成立。

综上可知，任意一个技能约束稳定匹配都是模型（6.7a）—（6.7i）的一个可行解，即U⊆Ω。证毕

依据引理6.1和引理6.2容易获得如下定理。

定理6.2 对于任意给定的HSM（1，1，n，1）问题，都有Ω⊆U。

（3）模型求解

模型（6.7a）—（6.7i）是一个双目标的0-1整数规划模型，本书采用ε-constraint方法进行求解[388，389]。ε-constraint方法解决双目标优化模型的基本思想是将其中一个目标函数转换为约束条件，从而将双目标优化模型转换为单目标优化模型进行求解。下面以目标函数Z2作为约束条件为例来说明ε-constraint算法的具体流程。

令S表示目标函数值集合，迭代步长为θ。

步骤1 计算模型的理想点（ideal point）和最差点（nadir point）。其中，和分别表示单独考虑目标函数Z1和Z2时的最大值，而和分别表示当目标函数Z2和Z1取得最大值时，目标函数Z1和Z2的函数值。

步骤2 。

步骤3 若，则转向步骤4；否则，转向步骤5。

步骤4 采用分支定界算法或优化软件包Lingo、Cplex等求解如下的单目标优化模型（6.13a）—（6.13i），获得最优解的函数值，且S=S∪，转向步骤3。

步骤5 删除S中被占优的点，获得帕累托前沿，算法结束。

依据ε-constraint的理论可知，模型（6.13a）—（6.13i）的每个最优解都是双目标优化模型（6.7a）—（6.7i）的帕累托解，因此，通过上述算法的不断迭代，可以获得双目标优化模型（6.7a）—（6.7i）的帕累托前沿。

综上所述，针对考虑服务技能约束的家政服务人员和雇主多双边匹配问题，本节给出的双边匹配方法的步骤如下：

步骤1 获得家政服务人员Wi给出的关于雇主Ej的偏好序rij、雇主Ej给出的关于家政服务人员Wi的偏好序tij以及家政服务人员Wi所具备的服务技能向量Pi、雇主Ej需要的服务技能向量Qj；

步骤2 通过式（6.5）和（6.6）分别计算家政服务人员Wi对雇主Ej的满意度αij和雇主Ej对家政服务人员Wi的满意度βij；

步骤3 依据家政服务人员满意度αij和雇主满意度βij，构建家政服务人员和雇主满意度最大为目标的双目标优化模型（6.7a）—（6.7i）；

步骤4 采用ε-约束算法将双目标优化模型（6.7a）—（6.7i）转换为单目标优化模型（6.13a）—（6.13i）；

步骤5 通过逐步迭代获得双目标优化模型（6.7a）—（6.7i）的帕累托前沿；

步骤6 决策中介根据实际需求从帕累托签约中选择最优稳定匹配方案。