国内某婚恋中介在某段时间内收到10位男士(A1,A2,…,A10)和6位女士(B1,B2,…,B6)提交的征婚交友信息。男士和女士在择偶时主要考虑对方的年龄、职业、相貌、身高、学历、性格、家庭背景、个人收入等,男士Ai对每个女士的基本情况进行综合评估后给出了6个女士的排序,如表5.1所示;类似地,女士Bj对每个男士的基本情况进行综合评估后给出了10个男士的排序,如表5.2所示。同时在现实生活中,若男士Ai把女士Bj排在更靠前的位置,例如男士Ai认为在6个女士中,女士Bj是最好的,由于心理因素的影响,女士Bj会由于男士Ai对自己更感兴趣而产生互惠偏好,相对于其他男士,女士Bj会给予男士Ai更高的互惠偏好;类似地,男士也具有互惠偏好。男士Ai和女士Bj给出的互惠因子分别如表5.3和表5.4所示。
表5.1 男士给出的偏好排序
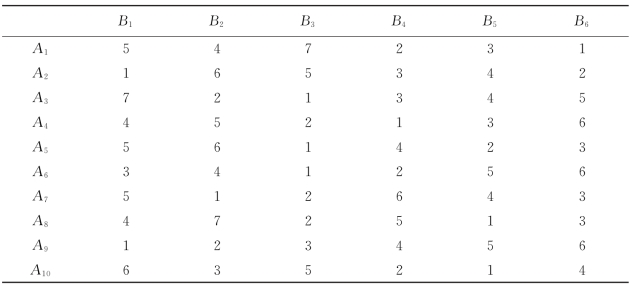
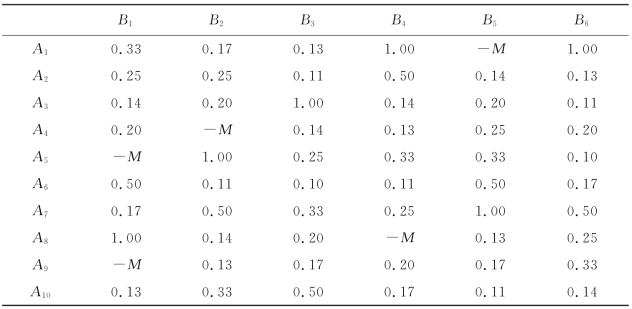
表5.2 女士给出的偏好排序
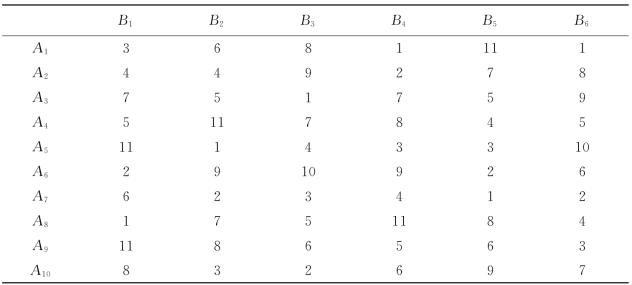
表5.3 男士互惠因子
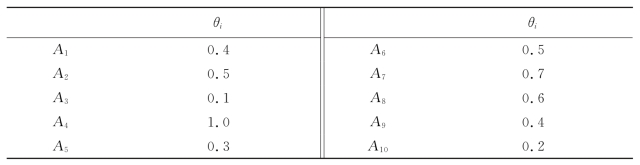
表5.4 女士互惠因子

下面采用本书提出的双边匹配决策方法来解决上述男士和女士婚姻匹配问题。
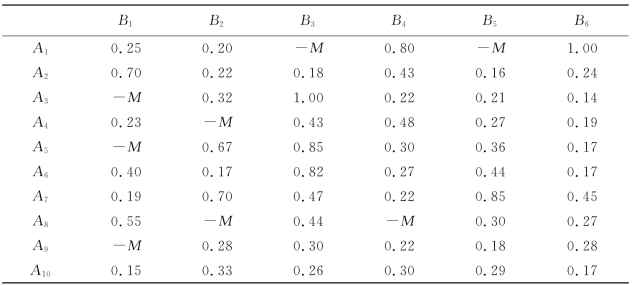
首先,依据表5.1和表5.2中男士和女士分别给出的对方偏好排序信息,采用式(5.1)和式(5.2)计算男士Ai对女士Bj的个体满意度p1(rij),如表5.5所示,以及女士Bj对男士Ai的个体满意度q1(sij),如表5.6所示。
表5.5 男士的个体满意度
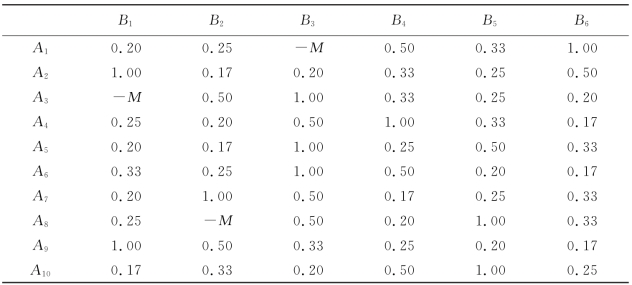
表5.6 女士的个体满意度
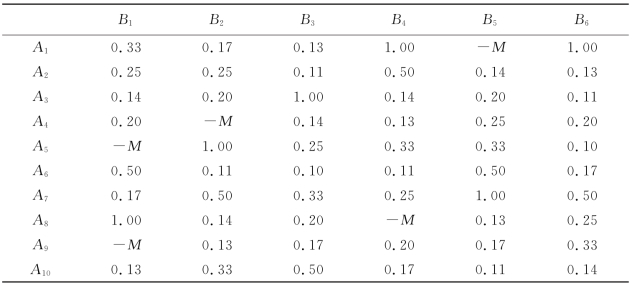
然后,依据表5.2中女士给出的男士偏好排序信息以及表5.1中男士给出的女士偏好排序信息,分别采用式(5.3)和式(5.4)来计算男士Ai对女士Bj的互惠满意度p2(sij),如表5.7所示,以及女士Bj对男士Ai的互惠满意度q2(rij),如表5.8所示。
表5.7 男士的互惠满意度
 (https://www.xing528.com)
(https://www.xing528.com)
表5.8 女士的互惠满意度
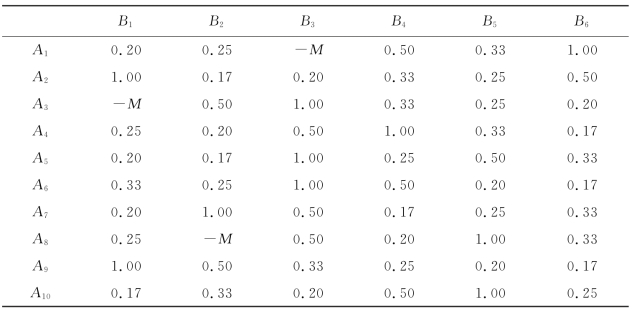
进一步地,依据男士和女士的个体满意度和互惠满意度以及男士和女士给出的互惠因子,采用式(5.5)和(5.6)分别计算男士和女士的总体满意度αij和βij,如表5.9和表5.10所示。
表5.9 男士的总体满意度
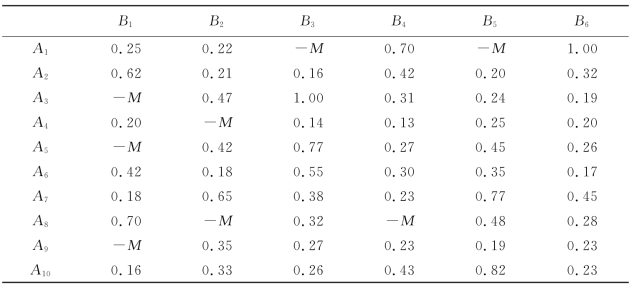
表5.10 女士的总体满意度
在此基础上,可以构建多目标优化模型(5.7a)—(5.7h),并采用本书提出的多目标优化模型求解方法进行求解,获得的最优稳定匹配方案为μ*={(A1,B6),(A2,B1),(A3,B3),(A4,B4),(A5,B2),(A7,B5)},即男士A1与女士B6进行匹配,男士A2与女士B1进行匹配,男士A3与女士B3进行匹配,男士A4与女士B4进行匹配,男士A5与女士B2进行匹配,男士A7与女士B5进行匹配。若不考虑男士和女士双方的互惠偏好,获得的最优稳定匹配方案为μ*={(A1,B6),(A2,B4),(A3,B3),(A5,B2),(A7,B5),(A8,B1)}。考虑双边互惠偏好和不考虑双边互惠偏好的对比分析结果,如表5.11所示。
从表5.11可以看出,考虑双边互惠偏好与不考虑双边互惠偏好获得的最优稳定匹配方案是不相同的,目标函数Z1和Z2的值也不相同,由此可以看出,双边主体的互惠偏好对双边匹配决策结果具有重要影响,在双边匹配决策过程中不能忽视这一因素。
表5.11 对比分析

本书对θi+λj=1时不同θi和λj的取值对双边匹配结果的影响进行了分析。由于本书算例规模比较小,当θi+λj=1时通过采用Lingo软件包求解优化模型(5.7a)—(5.7h)获得的最优匹配方案,如表5.12所示。
表5.12 求解优化模型获得的最优匹配方案

由表5.12可以看出,随着男士互惠因子θi的不断增加,女士互惠因子λj不断减小,男士和女士的总体满意度呈现先降低后增加的趋势,并且虽然θi和λj不同取值下获得的最优匹配方案有些是相同的,但是获得的总体满意度却是不同的,由此可以说明男士和女士的互惠因子对双边匹配决策的结果具有直接的影响。
当θi+λj=1时,采用贪婪算法获得不同θi和λj取值下的最优匹配方案,如表5.13所示。由表5.12和表5.13可以看出,在不同θi和λj取值下,通过贪婪算法和优化模型获得的匹配方案大部分是相同的,但也有部分是不同的,比如表5.7中的方案和表5.11中的方案,采用优化模型获得的匹配方案的总体满意度要大于采用贪婪算法获得的匹配方案,但当双边匹配问题规模比较大时,贪婪算法所具有的高计算效率是求解优化模型所不能比拟的,因此,针对θi+λj=1这种情形,需要决策者依据实际情况进行合理选择求解方法。
表5.13 贪婪算法获得的最优匹配方案

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




