算例分析：稳定匹配帕累托解的数量和约束条件的关系

国内某大型软件公司通过层层筛选录用了8名求职者（A1，A2，…，A8），经过短期培训后公司人力资源部门要将这8名求职者分配到全国不同地域的4个软件项目组（B1，B2，B3，B4），其中项目组需要的人员数量分别为：q1=2，q2=1，q3=3，q4=2。为了降低工作人员因对工作不满意而产生的离职率，提高求职者工作的稳定性，公司人力资源部门在分配过程中充分考虑求职者和软件项目组双方的偏好。求职者依据软件项目组的工作地域、工作环境、工资待遇等对软件项目组进行综合评价，求职者给出的不同软件项目的偏好信息为序区间偏好信息，如表4.1所示；软件项目组依据项目类型、项目需求的技能以及求职者的专业背景、实习或工作经历等对求职者进行综合评价，软件项目组给出的不同求职者的偏好信息为序区间偏好信息，如表4.2所示。公司人力资源部门依据软件项目组和求职者提交的偏好信息，采用双边匹配决策方法来获得最优匹配方案。

表4.1　求职者给出的关于软件项目组的序区间偏好信息

表4.2　软件项目组给出的关于求职者的序区间偏好信息

采用本书提出的双边匹配决策方法解决软件项目组与求职者双边匹配问题的计算过程如下：首先，依据求职者和软件项目组给出的序区间偏好信息，采用公式（4.1）—（4.3）和公式（4.4）—（4.6）计算得到求职者给出的软件项目组的排序位置与理想位置的相对贴近度，如表4.3所示，软件项目组给出的求职者的排序位置与理想位置的相对贴近度，如表4.4所示。

表4.3　求职者的相对贴近度

表4.4　软件项目组的相对贴近度

然后，依据表（4.3）和表（4.4）的信息，可以构建获得α-稳定匹配方案的双边匹配优化模型（4.7a）—（4.7 h）；最后，采用ε-约束算法求解α=1时的双目标优化模型。

依据ε-约束算法的流程，首先，计算单独考虑目标函数Z1和Z2时的最优解和对应的Z1的目标函数值为，Z2的目标函数值为3.63；对应的Z2的目标函数值为，Z1的目标函数值为。

然后，在ε-约束算法迭代过程中，若令迭代步长为θ=0.5，以目标函数Z2为约束条件，则获得的帕累托有效解如表4.5所示；若以目标函数Z1为约束条件，则获得的帕累托有效解如表4.6所示。在θ=0.5时，以目标函数Z2为约束条件与以目标函数Z1为约束条件获得的帕累托有效解的分布，如图4.1和图4.2所示。从图4.1和图4.2可以看出，帕累托有效解的分布还是比较均匀的。软件公司的人力资源部门可以根据具体需求选择合适的匹配方案，例如，若选择求职者最优的稳定匹配方案，则匹配结果为求职者A3和A5参与软件项目组B1、求职者A2参与软件项目组B2、求职者A6、A7和A8参与软件项目组B3、求职者A1和A4参与软件项目组B4。

表4.5　目标函数Z2为约束条件时的帕累托有效解(www.xing528.com)

表4.6　目标函数Z1为约束条件时的帕累托有效解

图4.1　目标函数Z2为约束条件的帕累托有效解分布

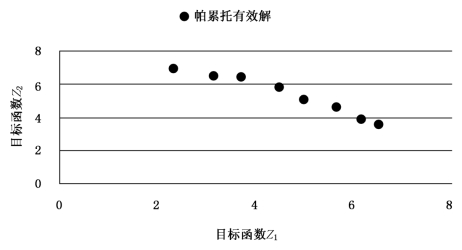
图4.2　目标函数Z1为约束条件的帕累托有效解分布

为了研究ε-约束算法中，迭代步长θ的不同取值对算法结果的影响，本书对迭代步长θ的取值与帕累托有效解的数量关系进行了探讨。在以目标函数Z2为约束条件的情况下，获得的稳定匹配帕累托有效解的数量与迭代步长θ的关系如图4.3所示。由图4.3可知，迭代步长θ取值越小，获得的帕累托有效解的整体变化趋势是越多的。然而，迭代步长θ取值越小，算法迭代的次数也就越多，从而获得帕累托有效解集合的计算时间也相应增加，因此，迭代步长θ取值需要决策者根据问题需要进行合理选择。

图4.3　迭代步长与帕累托有效解的数量关系

当α=1时，α-稳定匹配的帕累托有效解与稳定匹配的帕累托有效解是相同的，这是由于当α=1时，α-稳定匹配集合与稳定匹配集合是相同的。当α=2时，以目标函数Z2和Z1为约束条件获得的帕累托有效解分别如表4.7和表4.8所示。由表4.5、表4.6和表4.7、表4.8的对比中可以看出，α=1与α=2获得的帕累托有效解大部分是不同的。此外，α=1时获得的所有帕累托有效解中求职者的最高满意度为6.51，而α=2时求职者的最高满意度为6.67，这是由于随着α取值的增加，形成α-稳定阻塞对的条件越来越严格，从而α-稳定匹配的数量越来越多而造成的。

表4.7　目标函数Z2为约束条件时的帕累托有效解

表4.8　目标函数Z1为约束条件时的帕累托有效解