使用遗传算法求解公平稳定匹配数学模型

本书建立的公平稳定匹配数学模型是一类0-1型整数规划问题，如果问题规模比较小可以采用传统的求解方法如分支定界法、广义Benders分解法（GBD），外近似法等。但是由于随着问题规模的扩大，这些传统方法的计算量急剧增加，求解效率很低。本书依据建立的公平稳定匹配数学模型（3.6）的特点设计了一种求解该模型的遗传算法。遗传算法的具体步骤如下：

（1）个体编码和种群初始化

编码采用顺序编码方式，编码原理是染色体的固定位置表示甲方主体的编号，染色体上的每个基因代表乙方主体的编号。由于本部分研究的是一对一的双边匹配，因此个体基因不允许重复。对于甲方主体数量为m和乙方主体数量为n的双边匹配问题中m≤n，染色体的长度为m，个体编码如图3.1所示。种群初始化是从n个乙方主体中随机选择m个分配给m个甲方主体。

图3.1　个体编码

（2）适应度函数

如果种群的一个个体中甲方和乙方形成的匹配是稳定匹配，那么这个个体称为可行个体，否则称为不可行个体。本部分对可行个体与不可行个体采用不同的选择的方式，可行个体的适应度函数为

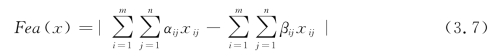
采用约束违反度作为不可行个体的适应度函数：

其中，F（x）表示个体x的非阻塞匹配对数量，约束违反度Inf（x）用于度量个体x到可行域的距离。约束违反度Inf（x）越大表示个体离可行域越远，反之越近。

（3）交叉算子

如果甲乙双方主体数目不同，假设m＜n，采用文献[370]提出的一种特殊均匀交叉算子，这种算子的最大特点是产生的后代个体都是合法个体，不需要进行修复。首先，查找两个父代个体P1和P2含有的相同基因有g个，g≤m，这g个基因在父代个体P1上的位置即甲方主体的位置编号组成集合D={d1，d2，…，dg}，1≤df≤m，f=1，2，…，g；g个基因在父代个体P2上的位置即甲方主体的位置编号组成集合T={t1，t2，…，tg}，1≤te≤m，e=1，2，…，g。然后令S=D∪T={s1，s2，…，sq}表示父代个体P1和P2的相同基因所对应的甲方主体编号组成的集合，1≤sl≤m，l=1，2，…，q。B1∈B表示在父代个体P1中与集合S中的甲方主体编号对应的乙方主体编号构成的集合，B2∈B表示在父代个体P2中与集合S中的甲方主体编号对应的乙方主体编号构成的集合。最后，将父代个体P1和P2中，甲方主体编号在S中的基因直接分别复制给子代个体C1和C2，将集合B\（B1∪B2）中的乙方主体编号随机分配给子代个体C1和C2的其余基因位置。

如果甲乙双方主体数目相同m=n，本书采用文献[379]提出的循环交叉算子进行交叉操作，循环交叉算子具有操作简单，不会产生不合法子代个体的优点，限于篇幅本书不再对循环交叉进行详细阐述。

（4）变异算子

本书根据甲乙双方主体数量的不同选择合适变异算子。如果甲乙双方主体数量不相同，假设甲方主体数量少于乙方主体的数量，即m＜n时，采用引入原来个体中不含有的新基因的变异方式。对于一个父代个体P，它的染色体上与甲方主体匹配的所有乙方主体构成的集合为B1⊂B。首先，随机选择染色体上一个基因位置r1，1≤r1≤m；然后从乙方主体集合B2=B\B1中随机选择一个乙方主体替换位置r1上的基因。如图3.2所示。

图3.2　引入新基因变异

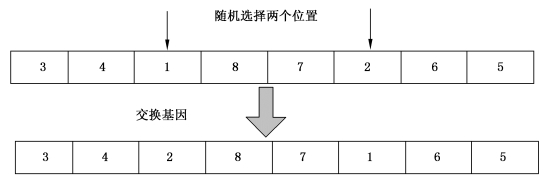
如果甲方主体数量与乙方主体数量相同，即m×n时，采用换位变异。对于一个父代个体P，换位变异是随机在染色体上选取两个位置r1和r2，1≤r1＜r2≤m，然后交换r1和r2两个位置的基因。显然，换位变异不会产生不合法的个体。如图3.3所示。

(www.xing528.com)

图3.3　换位变异

（5）选择策略

本书设计的遗传算法中，采用锦标赛选择策略。锦标赛选择每次从种群中随机选择t个个体，然后选择个体适应度值最好的一个个体进入子代种群，直到子代种群达到原来的种群规模。本书选择t=2作为锦标赛选择的竞赛规模。依据以下准则进行个体选择[19]：

（a）如果两个个体都是可行解，根据公式（3.7）选择适应度小的个体进入子代种群。

（b）如果一个个体是可行解，一个是不可行解，选择可行解个体进入子代种群。

（c）如果两个个体都是不可行解，根据公式（3.8）计算两个个体的约束违反度，选择约束违反度小的个体进入子代种群。

设种群规模为pop Size，种群最大迭代次数max Gen，交叉概率pc，变异概率pm，迭代次数t，种群P（t）。设计的多目标遗传算法的具体步骤如下：

步骤1 种群初始化。初始迭代次数t=0，随机产生pop Size个个体，从而得到算法的初始种群P（0）；

步骤2 计算种群个体的适应度值，并对当前种群进行锦标赛选择操作，从而产生一个新的种群P′（t）；

步骤3 对新种群P′（t）中满足交叉概率和变异概率的个体进行交叉和变异操作，产生新的种群P″（t）；

步骤4 将种群P（t）和P″（t）的个体进行合并，按照个体适应度从中选择出较优的pop Size个个体产生种群P（t+1）；

步骤5 令t=t+1。如果t＞max Gen，则算法停止，输出最终结果。否则，返回步骤3。

综上所述，针对基于多指标评价信息且考虑双边主体公平性的满意匹配问题，本章给出的双边匹配方法的步骤如下：

步骤1 依据Ai给出的Bj关于评价指标的Df满意度评价值以及Ai给出的关于指标Df的权重，采用式（3.1）计算Ai对Bj的满意度αij；

步骤2 依据Bj给出的Ai关于评价指标It满意度评价值以及Bj给出的关于指标It的权重，采用式（3.2）计算Bj对Ai的满意度βij；

步骤3 依据Ai对Bj的满意度αij和Bj对Ai的满意度βij，在考虑匹配稳定性的基础上，构建以双边主体满意度差异最小为目标的优化模型（3.6a）—（3.6e）；

步骤4 证明多目标优化模型中所确定的稳定约束条件（3.6d）的合理性；

步骤5 针对所建立模型的特点，设计了一个求解大规模双边匹配问题优化模型的遗传算法；

步骤6 采用设计的遗传算法求解模型获得双边匹配方案。