预测方法介绍：个人所得税

6.2.2.1　生长曲线预测法

生长曲线模型（growth curve models）指随着时间的推进，经济事务的观测值逐步推进，并且其推进方式符合生长曲线的一般规律。它按照事务发展各个阶段的特点，把事务发展分为以下三个阶段：萌芽阶段、成长阶段和发展成熟阶段。由于事务所处发展阶段不同，会表现出不同的发展规律。生长曲线法的应用极其广泛，它不仅可以描绘事务发展的基本趋势，还可以准确地预测事务由高速发展变为缓慢发展的转折时期，从而为事务发展规划提供决策。在现实中，一些经济现象的发展规律比较接近或者符合生长曲线模型，所以，在对一些经济现象进行分析时，可以考虑采用此种方法。

生长曲线的模型有很多，本部分采用的是生长曲线模型的一般形式。设y为预测经济目标的定量值，则生长曲线基本模型为

假设关于y的观测值为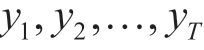。将T个数据平均分为3组，每组个数为n=T/3。设

整理并求解可得

为了便于计算，两边取对数，即

6.2.2.2　确定型常参数预测方法

确定型常参数预测方法因把预测值作为确定型变量而得名，通过建立确定型模型计算。假设，模型中的待定参数为未知数，预测变量和自变量为已知量，根据历史数据建立有关参数的方程组，方程个数由参数个数决定，通过求解方程即可得到最终预测模型。当参数值求出以后，假设参数为已知变量，预测值为未知变量完成今后年度的预测。

假设：y为预测值，xj为影响y的第j个自变量，yi为y的第i个观测值；xij为xj的第i个观测值。y与xj之间的函数关系为

其中，aj为待定常参数，衡量xj对y的影响关系与程度深浅。一般令x1=1，即a1为常数项，m≥2。

但是在实际当中，样本信息容量的局限性，再加上信息记录中随机性的存在以及人们认识的局限性，使得aj的真实值难以求出。为了获得aj的值，我们可以根据一些信息推断出其真实值的逼近估计值，我们通过以下模型完成估计：(www.xing528.com)

上式中包含了m个未知数，但是仅有一个方程，因此可能存在无穷多个解。为了增加方程个数从而求得唯一解，我们可以将上式中总偏差为零转化为局部偏差为零，也就是把n个历史数据分割为m段，割点循序依次为n1， n2，…，nm−1，则可得到下列方程：

整理得到下列公式一：

上面有m个未知数，m个方程，故可得唯一解，设唯一解为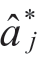，则估计模型为：

根据上述模型，当xj取历史数据xij时，可得到历史估计值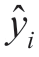，当xj取未来值时，则可得到未来预测值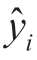，如第n+k期的预测值为

为了便于简单直观地计算求解，我们通过以下变形，将公式一变形为

每一个方程均除以相应的数据个数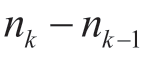，其中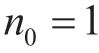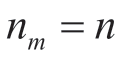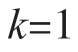，，，2，…，m，则得到

6.2.2.3　ES方法

ES方法与一般意义上的指数平滑平均预测方法不同，一般意义上的指数平滑预测方法仅为ES预测方法提供了基础工具。设预测对象变量为y，其时间序列资料为yi，真实的时间序列函数值为y （t）=f （t），yi围绕y （t）波动，f（t）为真实函数，依据泰勒级数原理，函数可以展开成自变量的m次多项式，即

通过进一步简化整理，最终的预测模型为