球面成像的实像与虚像的形成

2.2.3.1　近轴光线条件下球面发射的物像原理

由于折射面对称于光轴，所有自轴上点A发出的与光轴成相同夹角U的任一条光线，在像方都应交光轴于同一点。那么能否说A′点就是物点A被折射球面所成的像？否！

在图2.18中，若轴上物点A发出同心光束，由于各光线具有不同的U角值，所以光束经球面折射后，将有不同的L′值。也就是说，在像方的光束不和光轴交于一点，即失去了同心性。因此，当轴上点以宽光束经球面成像时，是不完善的，这种成像缺陷称为像差，是以后将会讨论到的球差。这个对于凸球面折射的物像原理也适用于凹球面折射，而且在近轴光线条件下不论S值的大小如何都能使用。

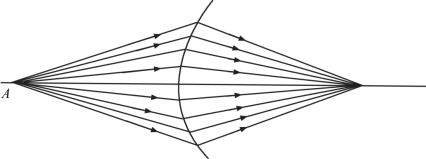
图2.18　单个折射球面成不完全像(www.xing528.com)

由于像可以是实的也可以是虚的，即可以位于球面的任一侧，所以像所在的空间可以从球面一侧的无穷远处伸展到另一侧的无穷远处。根据无限的共轭性，对于像的每一个位置，物都有一个相应的位置，因此物所在的空间也具有相同的变化范围。也就是说，物所可能存在的空间和像所可能存在的空的是完全重叠的。为了区分它们，我们规定入射光束在其中进行的空间为物空间，折射光束在其中进行的空间为像空间。对于单独一个球面来说，如光线自左向右进行，则物空间在球面顶点的左方；像空间在球面顶点的右方。此时物距应该取负值（S＜0）如折射光束在像空间会聚，像点就在顶点右方（S1＞0），所得到的是实像，如折射光束在像空间发散（S1＜0），所得到的是虚像。要注意虚像虽在物空间，但它并不实际存在，实际存在的是像空间的发散光束。

在球面反射的情况中，物空间和像空间相重合。在S＜0的情况下，S1＜0得实像，S1＞0得虚像。

2.2.3.2　高斯公式和牛顿公式

以后我们将看到，在其他光具组理想成像时，联系物距、像距和焦距的关系式也和上式完全相同。因此可说其是普遍的物像公式，称为高斯物像公式。应该指出，若光线自右向左进行，则物空间在球面顶点的右方，而像空间在球面顶点的左方。此时前述符号法则仍然运用，f1仍是方焦距，f仍是物方焦距，但此时物距应该取正值（S＞0）。如果折射光束在像空间会聚，像点在球面顶点左方（S1＜0），则得到的是实像，如果折射光束在像空间发散，像点在球面顶点右方（S1＞0），则得到的是虚像。

我们采用的这一符号法则，比较符合数学惯例（仅角度的正负方向照顾到应用光学的习惯），对于不同的光线方向也能适用，这个符号法则称为笛卡儿符号法则。