随机Leslie矩阵的理论模型

自从Leslie矩阵模型在解决生态问题方面得到很好的结果以来，Leslie矩阵模型也越来越多的用于建立人口动态模型。从数学的角度来看，Cohen团队和Arnold团队分别在1984年和1994年解决了进化系统中出现的一类随机矩阵的渐进行为。从这些前人研究的问题中，可知研究人口问题时一定要考虑一个重要因素，即可变性。因此，在生命参数相关随机性存在的情况下，如何描述年龄结构化种群的动态？即转化成数学问题为：是否可以根据投影矩阵的无序性进行一般的代数分析，以便于找到有效的人口增长率和渐近均值人口向量？这样，国外学者采用了随机Leslie矩阵来处理此问题。利用推广的种群增长率概念来分析生命参数不确定时的人口动态。通过处理线性非负随机矩阵差分方程来将均值人口向量的长期渐进动态的非平凡有效特征值定义为有效的增长率。这个有效特征值是从长期多项式的最小正根开始计算的。本章将利用变化增长率的随机Leslie矩阵模型来预测2019年到2050年的人口结构，在总和生育率加入了随机的因素。

考虑到人口增长率包含不确定性的情况，不确定中包含一些基本特征，例如女性的生育率，该参数的不确定性可以与一些随机变量相对应，因此投影矩阵M变为随机矩阵，并且随机矩阵M特征值λ1的研究是一个非平凡的问题。在Leslie的开创性工作中，投影矩阵的特定结构是根据与模型中时间步长相同的持续时间的年龄间隔。其中，将特定年龄的生育力参数fj放在矩阵的第一行，将特定年龄的生存概率Pj放在矩阵的次对角线上，将矩阵的其他元素设定为零（Caceres and Caceres-Saez，2011）。

考虑一个m×m的Leslie矩阵，其中矩阵中的每个元素是非随机变量且假定fj≥0，Pj∈[0，1]。

其中fj和是pj随机变量，且满足如下式子：

其中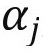和是Leslie模型中的随机变量。利用上式，将出生率和存活率这两个重要参数写成如下式子：

其中，和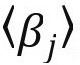表示平均值，所以，为均值为零的随机数，和非随机的正数。

人口的有限增长率是要研究的基本人口统计参数。使用年龄结构的Leslie模型，增长率由Perron-Frobenius特征值λ1给出。并且对特征值的估计必须考虑其不确定性，特别是在涉及政策的情况下。最重要的是置信区间是否包括λ1=1，其可以反映人口是随着时间减少还是随着时间增加这个现象。估计特征值的不确定性在很大程度上限于对生命率的敏感性分析。由于该矩阵的特殊结构，有可能应用到Perron-Frobenius定理，考虑到（如果不可约）非退化正特征值λ1的存在，并且满足。该特定的特征值λ1与一个正特征向量ψ1（平稳的人口向量）。因此，很容易证明由行为λ1n渐近控制的种群动态的稳定性。如果λ1＜1，那么稳定的人口以恒定的速率λ1下降；如果λ1＞1，那么稳定的人口以恒定的速率λ1上升。对于有序情况，Perron-Frobeniu定理可以有效地计算人口在矢量状态的渐近行为。研究人口的长期行为时，考虑n→∞时的人口结构即可。考虑以下形式的线性矩阵方程：(www.xing528.com)

其中，Xn是一个维数为的状态向量，用于计算时刻处的人口总量。人口向量中的每个分量Xn（j）代表每个识别类别j中的个数。fj→fj-aj且fj-aj≥0可以利用下面的生成函数来求解：

其中，生成函数G（z）是由人口状态向量Xn生成。

结合和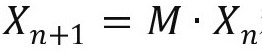，可以得到

根据上面的结果，引入恒等矩阵I，得到如下结果：

其中，格林函数G（z）是一个（m×m）矩阵，并且fj→fj-aj且fj-aj≥0中的人口动态信息包括在函数G（z）的极点中。在非随机的情况下，这些极点与矩阵M的特征值完全一致。