退休选择理论-中国人口变动与养老金可持续性研究

我们可以按惯例将人口分为劳动年龄人口（18～64岁人口）、18岁以下的年轻受抚养人和65岁以上的老年受抚养人。这些分组是为了说明替代生育率假设对人口年龄结构的影响。它们不应被视为试图从字面上定义劳动力；它们代表着通常或典型工作生活的代理人。如果生育率保持在每名妇女生育2.1个孩子，那么在未来75年内，劳动年龄占总人口的比例将在0.6左右波动。

生育率的降低持续低迷和死亡率的降低又重新激起了经济学家对老龄经济学的研究兴趣。结合对老年人收入状况的分析，形成了老龄化经济学的总体框架。养老保障计划的快速增长也一直是经济分析的重点。

2.2.5.1　退休选择理论的基本内涵

退休是富裕社会的报酬。回顾20世纪的饮食不良、恶劣的卫生条件加之一辈子的辛勤劳动，就可以解释为什么我们的先辈中很少有人活到了成熟的老年。事实上，在今天的一些发展中国家，这种不健康的状况仍然存在，大大减少了大多数人口存活至老年的机会。然而发达国家，人们的预期寿命在20世纪翻了一番，养老金覆盖面和保障力度也有所增加。长寿和财富增加的结合使越来越多的人期望在中老年从有偿工作中退休。事实上，许多国家的成年人在退休生活中花费了他们成年生活的三分之一到一半。

退休的概念比较复杂，因为它包含了富人，有时是老年人退出市场工作的非线性过程。特别是在发达国家，现代退休已经被等同于老年人的各种行为。例如，接受养老金或社会保障福利的行为、自愿或被迫离职、工作时间或工资减少、工作变动和劳动力退出等行为。

世界上的人口预期寿命不断延长，但退休时间更早，现在有大量的成年人一生中有三分之一的时间是依靠公共和私人退休福利度过的。因此，劳动经济学家对延迟或提前退休行为的因素非常感兴趣，他们试图了解人们为什么在年轻时离开工作岗位，雇主如何应对老龄化的劳动力以及退休对个人和社会的经济影响等。

斯托克和怀斯（Stock and Wise，1990）[101]基于继续工作的选择价值，建立了退休模型。继续工作的选择价值是该模型的核心特征。如果员工工作到一定年龄，通常是提前退休年龄，那么养老金计划规定会提供大量奖金，然后会有大量的诱因促使其离职。稍后退休的员工可以在不太有利的条件下退休。如果员工在提前退休年龄之前退休，则以后的奖金选项将丢失。继续工作保留了以后退休的选择，因此称为工作的“选择价值”。

该模型用于估计企业养老金计划准备金对退休的影响。该模型非常适合公司的微观退休数据，它能很好地捕捉到特定年龄阶段退休率的急剧不连续增长。例如，将提前退休年龄从55岁提高到60岁，将使50岁到59岁之间的公司离职率降低近40%。退休选择模型旨在捕捉一个重要的经验规律，即退休决定的不可逆性。虽然在退休后继续工作，至少是兼职，并不少见，但回到退休后的工作岗位却非常罕见。

该模型将重点放在退休的机会成本上，或者同等地，放在保留日后退休选择权的价值上。它有两个关键方面。第一，如果继续工作的选择价值大于立即退休的价值，那么一个人将在任何年龄继续工作。实际上，这个人将继续工作的选择价值与现在退休的价值进行了比较。第二，随着年龄的增长，个人会重新评估这个退休决定，因为更多的关于未来收入的信息以及未来退休福利会变得可用。例如，56～57岁的工资下降将导致个人重新评估未来的工资收入，从而重新评估未来的养老金福利和社会保障应计项目。因此，到了57岁退休似乎比56岁时更有利。退休是指继续工作的价值低于退休的价值。

可能存在一些可能会影响退休行为的个人属性，如养老金和社会保障财富以外的资产。因此，退休决策模型不考虑这种情况，它是基于工资收入和退休福利收入而进行选择的模型。

2.2.5.2　退休选择理论的主要框架

本节主要简要概括斯托克和怀斯构建的退休选择模型，简称Stock—Wise model。考虑一个在t年开端尚未退休的个体，由于具有理性预期，他只要继续工作，将在S年获得工资收入Ys；如果他选择在s年退休，他将获得退休真实的退休福利Bs。记r为该个体退休的第一个全年，即该个体没有工资收入的第一年。退休福利依赖于该个体的退休年龄、工作年限、工资收入记录，可以简记为Bs（r）。

为了构建退休决议模型，假设个体效用函数由两部分构成：工作收入效应Uw（Ys）和退休时的养老金福利Ur[Bs（r）]。

该个体在决定是否退休时，赋予未来收入效应一个贴现因子（discount factor）和他将在S年的死亡概率。如果他在r年退休，则其收益现值为：

因此，价值函数（value function）Vt（r）依赖于未来收入流和退休福利，而退休福利又依赖于他退休时的年龄r。

该个体在t年可以选择继续工作，因此r＞t；或者选择退休，则r=t。

在t年，该个体基于可得信息存在一个关于未来环境的期望为Et（·）。因此，如果该个体选择延迟退休到r年，则其期望收益为：

一般来说，个体退休年龄为65岁，因此，考虑该个体在t+1年和t+65岁之间考虑退休。记最高期望收益的退休年龄为r*，也即r*为

的最优解。如果该个体继续工作未获得期望收益，则选择退休，即(www.xing528.com)

同理，如果该个体继续工作获得了期望收益，则选择延迟退休，也即：

其中，r＞t。

假设效用来源于存在常数风险偏好形式的年度收入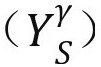和养老金福利收入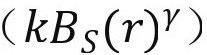，以及随机扰动项；且扰动项独立分布于收入和年龄，则：

其中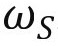，和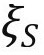是个体特定的随机效应，反映了影响退休决议的其他未观测因素。例如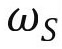，和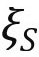可能反映了个体对工作—闲暇的偏好；或者反映了个体的身体健康状况。

假设此种随机效应具有不随时间变化的持久性，例如伤病影响了工作，产生了一个负的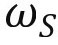，则后期也会产生一个负的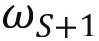，即个体随机效应服从马尔科夫或一阶自回归过程：

根据经验数据S=t+1，……，S，设定P=1，个体随机效应按照随机游走（random walk）演化。在时间S，个体知晓Ws和ζs，但是不知道它们在S+1及其随后时间的取值，对其预测服从以上方程。

通过简单合并与简化可知延迟退休的期望收益：

其中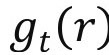，不同于，因为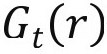包含了随机游走成分。如果该个体的生存概率独立于他的收入流和个体随机效应，则

其中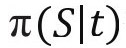，明该个体在t年存活至S年的生存概率。由于个体随机效应服从马尔科夫或一阶自回归过程

其中，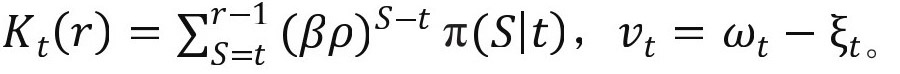

因此，联合以上方程可知：

由此，通过以上方程，可以进一步计算该个体在任一年份退休的概率。该个体的退休决议将通过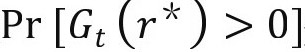来决定。

斯托克和怀斯[102]基于继续工作期权价值构建的退休选择模型表明如果将来选择一个更好的退休年龄比现在退休的价值更值钱，那么一个人就会继续工作。该模型综合了退休决策非线性预算约束和连续时间风险模型公式的优点。个体随机效应的马尔科夫链，或其随机游走，是该模型的重要组成部分。对替代养老金计划影响的模拟表明，计划准备金对退休率有非常显著的影响。他们的数据拟合表明将提前退休年龄从55岁提高到60岁将使50岁之前离开公司的员工比例减少近40%。

因此，在人口老龄化背景下，退休选择模型的重要政策内涵在于通过提高继续工作的选择价值和收益或者减少提前退休的福利待遇激励劳动力继续留在劳动力市场，主动选择延迟退休，从而缓解养老金压力，提高社会保障资金的可持续性。

伯克温科和斯特恩（Berkovec and Stern，1991）[103]提出了另一种建模退休的动态规划方法，他们使用模拟矩的方法来估计退休行为。他们允许个体存在三个状态：全职工作、兼职和退休。

此外，与斯托克和怀斯框架不同，退休并不是一种吸引人的状态；相反，在退休时，个人会选择每个时期，是继续退休，还是开始一份新的全职或兼职工作。Berkovec-Stern模型非常重要，因为它允许未来的不确定性进入动态规划模型。由于篇幅所限，本节不再赘述。

综上，退休决策关乎老年人退休后的收入乃至整个宏观经济的劳动力供给、养老金保障和经济增长等重要问题，研究延迟退休必然涉及老年人的退休选择问题。因此，退休选择理论为本书的研究主题提供了思想源泉。