Leslie矩阵模型及其优化

人口预测指的是在一定的范围内，根据人口现状、所处环境以及最重要的是人口的相关参数（出生率、死亡率、出生性别比、年龄特征等）做出假定，采用某种预测模型，对未来的某个时间段的人口结构、现状和趋势作出预测[89]，人口预测准确的结果可以为某地区的社会经济发展提供重要参考。人口预测的方法有很多，例如回归分析模型、ARMR模型预测、Logistic增长模型、BP神经网络预测、Leslie矩阵模型等（余爱华，2003）[90]。其中，Logistic增长模型的建模原理是人口发展按照指数增长函数变化，并且假定人口自然增长率为确定值，但是由于社会自然环境的容纳能力有限，人口增加的速度越来越慢，最后会达到人口的最大极限值。这个模型解决了在人口发展过程中增长率随时间变化的预测问题，即优势在于模型简单方便，适用于预测人口发展递减的时期。但这个模型存在一些缺陷：众所周知，影响人口增长的因素繁多，例如初始人口总量、社会环境、人口的生育政策等，所以最大人口容纳量的界限难以确定[91]。

回归分析模型预测法是将所有影响人口增长的因素联系起来，建立变量之间的回归方程，比较通俗易懂，但回归分析模型的难点在于无法将所有影响人口系统发展的因素全面的列举出来，无法选取这些指标来做定量分析，其只适合于中短期的人口预测，不适合于中长期的人口预测（甘蓉蓉和陈娜姿，2010）[92]。

ARMA模型（自回归移动平均模型）是通过历史的人口时间序列数据来揭示人口随时间变化的规律，并且将这些规律应用到未来，从而对未来的人口结构作出预测（陈爱平和安和平，2004；吴家兵和叶临湘，2006；任强和侯大道，2011）[93][94][95]。ARMA模型的前提之一是历史的时间序列数据是随机和平稳的。但在现实情况中，非平稳的时间序列居多，所以利用ARMA模型预测时要克服这一难点。

BP神经网络模型预测是利用大量的、不明确和随机的数据去发现人口发展的潜在规律，能够解决一些人口预测模型中的随机因素，实现原理将原始序列作为输入值，预测结果作为输出值，在模型运算过程不断地对输入变量进行误差修正，以便于最终的结果逼近于实际变化规律。（吴劲军，2004；尹春华和陈雷，2005）[96][97][98]但由于大量的历史数据难以获取，而且BP神经网络操作比较烦琐，所以预测结果精确度不高。

Leslie矩阵模型是按照性别分组，将某一时期的女性初始人口作为一个列向量，通过不同年龄组的生育率、不同年龄组死亡率构建一个Leslie矩阵，然后左乘分年龄组别的人口数量列向量，从而得到下一期的女性人口的列向量，最后再通过男女性别比来估计总人口的数量。人口规模发展的趋势变化不仅与出生率和死亡率密切相关，而且离不开各类人口数量、性别比例和年龄结构特征等因素的影响。Leslie矩阵人口模型能够将这些影响因子较全面地考虑到人口预测模型中。

从以上的模型的简单描述可以看出，回归分析模型、ARMA模型、Logistic增长模型、BP神经网络模型都只是对人口总量作出预测，但不能直接的、全面的预测分析未来人口的其他指标。相反，Leslie矩阵模型按照年龄、性别、出生率、死亡率等人口结构来进行预测分析，既可以将人口总量预测出来，也可以将各年龄段人口指标模拟出来。该模型在运行过程中层次清晰，可以多种情况一起进行预测，在预测中长期的人口规模中优势突出。

Leslie矩阵模型预测人口的具体步骤如下：

将人口按年龄大小等间隔地划分为个年龄组，同时对时间离散化处理，其单位与年龄区间的间隔相同[99]，这样便于讨论在不同时间段内人口的年龄分布。离散的时间t=0，1，2，……。设在时间段t内，第i年龄组的人口数量为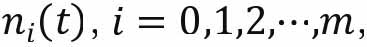定义向量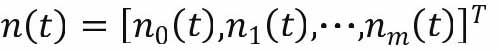。假设各年龄组之间的比率在一段时间内保持不变，故我们只考虑女性的人口分布n（t）随着时间t变化的规律，进而研究中国的人口规模。

设在单位时间内第年龄组女婴的出生率为bi，在单位时间内第年龄组女性的死亡人数占总人口数的比例为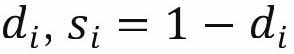，即在单位时间内第i年龄组存活的女性人数占总人口数的比例。假定bi、di、si不随时间t变化，根据上述参数的定义，t时刻的人口数量ni（t）和t+1时刻的人口数量ni（t+1）满足如下关系：

在上述式子中，假定bi表示扣除了在t时刻到t+1时刻出生但没有存活的女婴的比例。故我们可构造Leslie矩阵如下式所示：

根据Leslie矩阵，将t时刻和t+1时刻人口数量关系式改写为：

当L、n（0）已知时，对任意的t=1，2，……，有：

其中且至少有一个bi大于零。从上述的式子可以得出，矩阵L称为Leslie矩阵，根据Leslie矩阵和人口分布的初始向量n（0），可以模拟出女性人口分布n（t）的变化规律，进而得出不同年龄段人口总数的变化规律[100]。(www.xing528.com)

假定以0岁为起点，每1岁为一个年龄组。其中100岁及100岁以上为一个单独的年龄组。假设人口分布的初始向量为，其表达式为：

其中上标（0）表示预测的起点，下标表示从预测的起点开始划分的等间隔年龄组，这里，我们设置的是以1为公差的等差数列。该向量中共有101个元素，其中前100个元素表示每个等间隔年龄组的女性数量，最后一个向量元素表示100岁及100岁以上的女性数量。

存活矩阵如下所示：

其中Sx为各年龄组女性的存活率。

从预测起点开始，等间隔年龄组的女性人口数量矩阵由下式表示：

出生矩阵如下式所示：

其中bx表示等间隔年龄组的生育率。

由于我们已经给出存活矩阵和出生矩阵的形式，因此，Leslie矩阵可由下式给出：

初始的女性人口数量向量为p（0），五年后的女性人口数量向量可由下式表示：

依次类推，若初始人口为p（n），n+1年后女性的人口数可由下式表示：

这样，根据Leslie矩阵模型可知，在对人口预测分析中将会用到人口总量、人口预期寿命、出生人口性别比、总和生育率、年龄组间的存活率等指标，在已有年份的相关数据条件下，就可以对未来人口数量、人口抚养比等指标进行预测。