世代交叠模型是分析人口变动与养老金可持续性的重要理论基础,本节将主要分析世代交叠模型的基本涵义、世代交叠模型的主要特征和经济学含义。
2.2.2.1 世代交叠理论基本涵义
当代宏观经济学在分析消费—储蓄、劳动—闲暇等跨期决策及其长期一般均衡效应时存在两个主要分析框架,即世代交叠模型(overlapping generations model, OLG)和代表性组织模型(representative agents model)。世代交叠模型主要分析在同一时间生活的不同世代的交互效应,与此同时,新的世代不断进入生活决策;而代表性组织模型假设家庭部门由具有无限寿命的有限数量个体组成,因此,个体是同质的。世代交叠模型有助于分析生育决策、人口老龄化、公共债务、养老金筹资等问题,本书的个体由不同年龄群体构成,且主旨在于养老金筹资问题,因此主要分析框架为世代交叠模型。
代表性组织或者代表性家庭模型主要假设家庭生活无限期,效用主要来源于消费和闲暇,家庭需要做出消费—储蓄、劳动—闲暇等决策。代表性家庭模型可表达如下:
预算约束为,
其中,ct为消费,lt为劳动供给,wt和rt分别为工资和利息率,β为贴现因子(0<1<β),B>0代表了家庭的借贷约束。
由此,由一阶条件可得,
该式表明劳动和闲暇的边际替代率等于工资。
该式为消费的跨期欧拉方程。
建立在一个有代表性的家庭基础上的劳动力供应和储蓄理论有许多局限性,包括对于涉及异质性的问题以及家庭间的不平等。当然,原则上简化假设没有什么错,毕竟,模型是用来简化现实的表示。然而,当模型的某些驱动力随着时间的推移而发生变化,从而实质性地改变宏观经济行为时,代表性家庭模型不能分析不同年龄阶段的经济决策。
世代交叠模型得益于美国经济学家费雪《利息理论》的启发。1958年保罗·萨缪尔森(Paul Samuelson)[79]发展了世代交叠模型,彼得·戴蒙德(Peter Diamond,1965)[80]将新古典主义总产量生产函数纳入该模型中。当代,加里(Galor,1992)[81]和威尔(Weil,1996)[82]等人进一步发展了OLG模型[83]。
2.2.2.2 世代交叠理论主要特征
世代交叠模型相较代表性组织模型的独特特征主要在于以下三个方面:
第一,家庭部门的生命周期行为决策。在世代交叠模型中,尽管经济体是无限存续的,但个体的生命却是有限的。在个体的生命周期内,其教育水平、工作能力、收入水平、消费偏好将在个体的劳动—闲暇、消费和储蓄决策中。世代交叠模型的分析重点就在于个体生命周期行为决策。
第二,世代交叠模型的中心在于个体异质性,年轻人与老年人、工作者与退休者、当前一代与未出生一代等。因此,世代交叠模型可以研究关于不同世代的财富和收入分配问题。
第三,由于个体异质性,世代交叠模型分析其动态交互作用时存在复杂性。然而由于个体的有限生命周期,世代交叠模型的分析主要是一维的(one-dimensional),即主要分析模型的一阶差分方程,因此也存在简单性。在代表性组织模型中,由于个体同质性,分析其动态交互作用时,有其简单性,但由于个体的无限生命周期行为,其分析框架是二维的(two-dimensional),即不仅分析模型的一阶差分方程,还将分析其二阶或无穷阶。
简而言之,世代交叠模型在很多方面不同于代表性组织模型。在代表性组织模型中,经济行为个体的总量效应只是代表性个体行为的简单加总,因为个体是同质的。然而世代交叠模型不同,其总效应是不同个体在不同生命阶段不同行为相互作用的结果,不能对其简单加总,而且人口总量及其结构将发挥重要作用,影响经济体的长期效应。
2.2.2.3 世代交叠理论基本结构
(1)基本假设
世代交叠模型把时间分为具有平等长度的时间单元,假设个体生活为两期(年轻期和老年期),两期之间长度一般为30年,而经济体可以存续无限期。
该封闭经济体在t期年轻人数量 t=0,1,2,……,其中n为常数,可以理解为生育率或人口增长速度,且n>-1。因此,Lt为正数。
t=0,1,2,……,其中n为常数,可以理解为生育率或人口增长速度,且n>-1。因此,Lt为正数。
在该封闭经济体中,只有年轻人工作和储蓄,而老年人退休和消费。每个年轻人供给一单位劳动,即劳动力供给无弹性。由此,劳动和闲暇外生于经济模型。
在该封闭经济体中,产出是同质的,产出既可以用来消费也可以用来投资物质资本。物质资本是经济体中的唯一资产,家庭拥有物质资本,并向企业投资收取租金,货币在世代交叠模型中仅是一层面纱,可以忽略不计。
而且企业的技术是规模报酬不变的,该封闭经济体由三个完全竞争性市场组成:产品市场、劳动力市场和资本市场(孙烽和寿伟光,2001)[84]。
(2)家庭部门
在该经济体中,每一期存在两代人存活,即年轻期和老年期。年轻人向企业供给劳动,使用资本进行生产。年轻人为退休而储蓄,因此进入老年期时,动用储蓄进行消费。由此,经济体中的净投资可能为正。
家庭部门将储蓄直接投资于资本市场并向企业收取租金。假设同质产出可以量化,租金率记为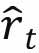 ,因此,一单位物质资本Kt的所有者将收取:
,因此,一单位物质资本Kt的所有者将收取:
其中,为资本的折旧率,假定为常数, 。
。
假设该经济体存在一个有效的贷款或债券市场,在t-1期到t期,家庭部门借出一单位产出,贷款市场的真实利率为rt,则在t期结束时,该家庭部门将获得1+rt单位的产出。在不存在不确定性的条件下,一般均衡条件要求资本市场和贷款市场的回报率相同。
由此,存在:
无套利条件表明在市场均衡时,资本市场的真实租金率等于贷款市场的真实利率。尽管在该OLG模型中不存在贷款市场,但是根据传统设定,称rt为真实利率。
家庭部门的效用函数为:
家庭预算约束为:
其中,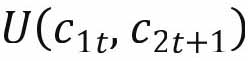 为生命周期效用函数,而
为生命周期效用函数,而 和
和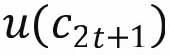 分别为年轻期和老年期的效用函数,为一期效用函数。效用函数为二阶可导的连续函数,其中,一阶导大于0,而二阶导小于0,表明边际效用为正,但边际效应递减。
分别为年轻期和老年期的效用函数,为一期效用函数。效用函数为二阶可导的连续函数,其中,一阶导大于0,而二阶导小于0,表明边际效用为正,但边际效应递减。
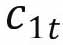 为每个年轻人在期的消费,包含了该年轻人子女的消费,
为每个年轻人在期的消费,包含了该年轻人子女的消费, 为年轻人进入老年时期即t+1期的消费;
为年轻人进入老年时期即t+1期的消费; 为时间贴现率,即对未来的不耐心程度;
为时间贴现率,即对未来的不耐心程度;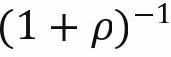 效用贴现因子,当偏好表现为以上形式,说明时间是可分的。
效用贴现因子,当偏好表现为以上形式,说明时间是可分的。 和
和 分别为年轻人在期的储蓄和工资;
分别为年轻人在期的储蓄和工资;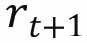 为t期到t+1期预期或期望的真实利率,由于经济主体存在理性预期,期望利率和真实利率并无区别。
为t期到t+1期预期或期望的真实利率,由于经济主体存在理性预期,期望利率和真实利率并无区别。
利率是储蓄的回报,也可以理解为未来消费的贴现率。由此,两期跨期约束可以转化为一个跨期预算约束:
在家庭预算约束下可对家庭效用函数进行最优化,从而得到家庭的消费和储蓄决策。
由一阶条件可得消费欧拉方程:(https://www.xing528.com)
消费欧拉方程表明储蓄的边际效应成本等于边际效应收益。
可将上式重复表述如下:
该式左边表老年消费相对于年轻期消费的边际替代率(MRS),即t+1期消费的增加必须依靠期消费的减少来弥补。
(3)生产部门
虽然世代交叠模型是一个长期动态模型,但本章理论基础进行简化,忽视技术变迁,并简化为一部门经济体。
在该封闭经济体中存在一个代表性企业,使用规模报酬不变的新古典生产函数生产最终品,由于企业的同质性,可以省去下标t。
 资本密集度;资本的调整和安装等成本忽略不计。
资本密集度;资本的调整和安装等成本忽略不计。
其中,生产函数的一阶导大于0,二阶导小于0。Y为最终产品,K和L分别为资本和劳动;另外,资本的动态方程可表达为:
该式表明,该经济体在t-1到t期的资本存量等于上一期资本存量减去折旧并加上一期的投资。
企业的利润函数可表达为:
由此,企业在最大化利润或最小化生产成本的条件可得:
其经济含义为企业将使用资本进行生产直到资本的边际产品等于市场租金率;企业将使用劳动进行生产直到劳动的边际产品等于工资。
(4)要素市场出清
该经济体存在三个市场:产品市场、资本市场和劳动力市场。资本市场和劳动力市场为要素市场,记Kd和Kd分别为资本和劳动的总需求。
由此,该经济体在t期,要素市场出清需要:
其中,Kt为资本的供给总量;Lt为劳动的供给总量。
该经济体均衡时,存在:
其中,Kd为资本需求密度。
根据
可知:
(5)经济体的动态路径
世代交叠模型的制度背景为产权清晰的完全竞争市场环境,存在一个序列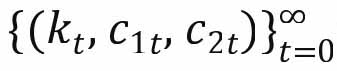 随着时间的流逝进行着不同的分配。
随着时间的流逝进行着不同的分配。
该经济体的技术可行性路径表明在技术和外生志愿给定情况下经济体动态的动态路径。该经济体存在两个外生资源:劳动,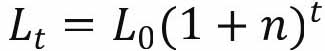 ;初期的资本存量K0。
;初期的资本存量K0。
记总消费为Ct
记总储蓄为St,存在
在封闭经济体中,总储蓄等于事后的总投资,即存在:
因此,存在
记Ct为每单位劳动的消费,则存在:
由此,该经济体的动态资源约束为:
产品市场出清要求:
其中,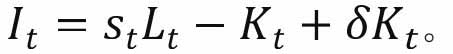
该经济体的均衡路径也称为跨期均衡,需要一系列条件满足:
技术可行性路径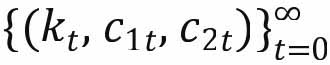 在
在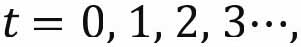 时,状态变量
时,状态变量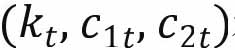 在期望利率等于真实利率的条件下存在暂时性均衡。
在期望利率等于真实利率的条件下存在暂时性均衡。
世代交叠模型的一个重要方面是,与第一福利定理保证帕累托效率的一般均衡模型相比,稳态均衡可以不是有效率的。因为经济体中的组织数量是无限的(未来时间的总和),资源的总价值是无限的,所以可以通过将资源从每一个年轻一代转移到当前的老一代来进行帕累托改进。
世代交叠型模型的另一个特点是,当资本积累增加到模型中时,可能会出现“过度储蓄”,这种情况可以由社会计划者通过强制家庭减少资本存量来改善。然而,对生产和消费技术的某些限制可以保证储蓄的稳态水平与索洛增长模型的黄金法则储蓄率相一致,从而保证跨期效率。
世代交叠模型的另一个基本贡献是,它们证明货币作为交换媒介的存在是合理的。一个期望系统作为一个平衡存在,在这个平衡中,每一个新的年轻一代都接受上一代的钱来交换消费。他们之所以这样做,是因为他们希望在老一代的时候能够用这些钱来购买消费品。
世代交叠模型可以有效地研究生命周期行为(人力资本投资、工作—退休和储蓄)、跨期资源分配(如社会保障)对长期人均收入的影响、经济增长过程中的决定因素及导致生育能力转变的因素。因此,世代交叠模型为研究延迟退休与养老金关系提供了主要的理论基石。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




