高等数学（二）全真模拟试卷第四套

一、选择题：本大题共10个小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的，选出正确选项。

A.0 B.1 C.e−1 D.+∞[ ]

2.当x→0时，ln（1+ax）是2x的等价无穷小量，则a=

A.−1 B.0 C.1 D.2[ ]

3.已知f（x）=xe^x+1，则f'（x）=

A.xe^x B.（x−1）e^x C.（x+1）e^x D.（x+1）e^x+1[ ]

4.已知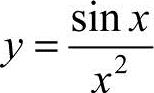，则y'（1）=

A.0 B.1

C.cos1−2sin1 D.cos1+2sin1[ ]

5.曲线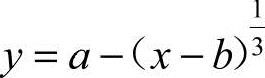的拐点坐标为

A.（a，0） B.（a，−b）

C.（a，b） D.（b，a）[ ]

6.已知f（x）的一个原函数为x²e^x，则∫f（x）dx=

A.4x²e^x+C B.2x²e^x+C C.x²e^x+C D.[ ]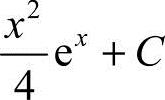

7.下列广义积分收敛的是

8.函数f（x）在[a，b]上连续是f（x）在该区间上可积的

A.必要条件，但非充分条件 B.充分条件，但非必要条件

C.充分必要条件 D.非充分条件，亦非必要条件[ ]

9.设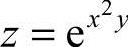，则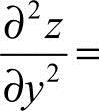

[ ]

10.对函数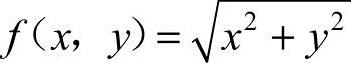，原点（0，0）

A.是驻点，但不是极值点 B.是驻点且是极值点

C.不是驻点，但是极大值点 D.不是驻点，但是极小值点[ ](www.xing528.com)

二、填空题：本大题共10个小题，共10个空，每空4分，共40分。把答案填在题中横线上。

11.当x→0时，若sin³x～x^a，则a=.

12.设f（x）是可导的偶函数，且f'（−x₀）=k≠0，则f'（x₀）=____.

14.函数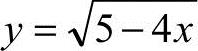在区间[­1，1]上的最大值是.

17.设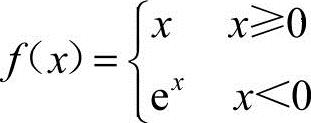，则∫²_-1f（x）dx=____.

18．设f(x)=_o^xln(t²+l)dt,则f¹(x)=____．

19.设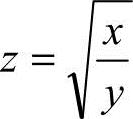，则dz=____.

20.设事件A与B相互独立，且P（A）=0.4，P（A+B）=0.7，则P（B）=.

三、解答题：本大题共8个小题，共70分。解答应写出推理、演算步骤。

21.（本题满分8分）计算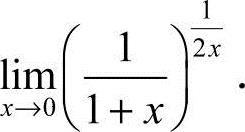

22.（本题满分8分）设f（x）=xln2x，且f′（x₀）=1，求f（x₀）.

23.（本题满分8分）计算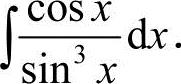

24.（本题满分8分）计算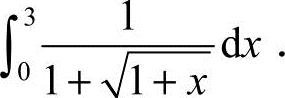

25.（本题满分8分）袋中有10个乒乓球。其中，6个白球、4个黄球，随机地抽取两次，每次取1个，不放回。设A={第一次取到白球}，B={第二次取到白球}，求P（B│A）.

26.（本题满分10分）设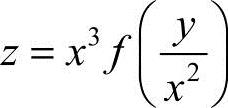，其中f为可微函数.

证明：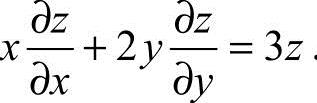

27.（本题满分10分）求曲线y²=2x+1，y²=−2x+1所围成的区域的面积A，及此平面图形绕x轴旋转一周所得旋转体的体积Vx.

28.（本题满分10分）设函数f（x）满足下列条件：

（1）f（0）=2，f（−2）=0.

（2）f（x）在x=−1，x=5处有极值.

（3）f（x）的导数是x的二次函数.

求f（x）.