高等数学专升本全真模拟试卷（第二套）

一、选择题：本大题共10个小题，每小题4分，共40分。在每小题给出的四个选项中，有一项是符合题目要求的，选出正确选项。

1.当x→0时，若sin²x与x^k是等价无穷小量，则k=

A.B.1 C.2 D.3[ ]

2.f（x）=x−2在点x=2的导数为

A.1 B.0 C.­ 1D.不存在[]

3.设f（x）=x^a+a^x+lna，（a>0且a≠1），则f'（1）=

A.a（1+lna） B.a（1−lna） C.alnaD.[ ]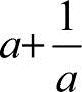

4.过曲线y=x+lnx上点M₀的切线平行于直线y=2x+3，则切点M₀的坐标是

A.（1，1） B.（e，e）

C.（1，e+1） D.（e，e+2）[]

5.下列命题正确的是

A.无穷小量的倒数是无穷大量 B.无穷小量是绝对值很小很小的数

C.无穷小量是以零为极限的变量 D.无界变量一定是无穷大量[]

6.已知函数f（x）=x³，则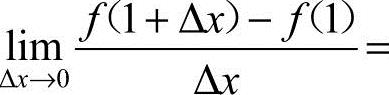

A.−3 B.0 C.1 D.3[]

8.设∫f（x）dx=e−2x+1+C，则∫f（2x+1）dx=

A.e−2x+1+CB.−e−2x+1+CC.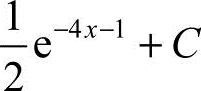D.[ ]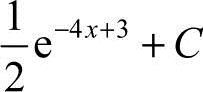

9.设z=e^xy，则dz=

A.e^xydx B.（xdy+ydx）exy

C.xdy+ydx D.（x+y）e^xy[ ](www.xing528.com)

10.3个男同学与2个女同学排成一列，设事件A={男女必须间隔排列}，则P（A）=

二、填空题：本大题共10个小题，共10个空，每空4分，共40分。把答案填在题中横线上。

12.函数y=ln（1+x²）的单调递减区间是____.

13.设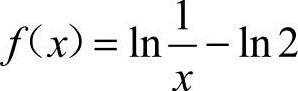，则f′（1）=.

14.曲线y=（x−1）3−1的拐点坐标是____.

15.设y=x³+e−2x，则y''=.

17.设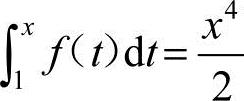，则∫²₁f（x）dx=.

19.已知f（x）≤0，且f（x）在[a，b]上连续，则由曲线y=f（x）、x=a、x=b及x轴围成的平面图形的面积A=.20.设z=f（x²+y²），则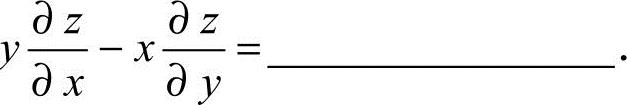

三、解答题：本大题共8个小题，共70分。解答应写出推理、演算步骤。

21.（本题满分8分）曲线y=f（x）过原点，且在点x处的切线的斜率为4x，求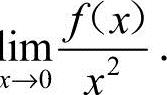

22.（本题满分8分）设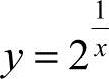，求y′.

23.（本题满分8分）计算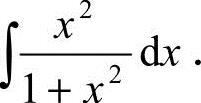

24.（本题满分8分）计算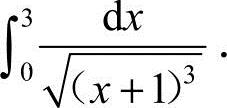

25.（本题满分8分）设随机变量ξ的分布列为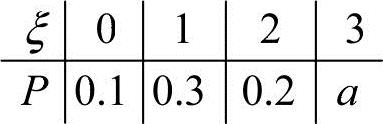，求a的值并求E（ξ）.

26.（本题满分10分）证明双曲线y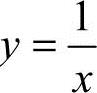上任一点处的切线与两坐标轴组成的三角形

的面积为定值.

27.（本题满分10分）求函数z=x²+y²−xy在条件x+2y=7下的极值.

28.（本题满分10分）建一面积为A的网球场（如下图所示），四周要留下通道，南、北两侧的通道宽为a，东、西两侧的通道宽为b.

问：为使征用的土地最少，则网球场地的长和宽各为多少？