证券投资组合的风险与报酬分析

投资者在进行证券投资时，一般并不把其所有资金投资于一种证券，而是同时持有多种证券。这种同时投资于多种证券的方式，称为证券的投资组合，简称证券组合或投资组合。由于投资组合能够分散风险，因此，绝大多数法人投资者如工商企业、信托投资公司、投资基金等都同时投资于多种证券。即使是个人投资者，一般也持有证券的投资组合而不只是投资于某一个公司的股票或债券。所以，了解证券投资组合的风险与报酬有助于企业财务人员理解证券组合的基本理论，恰当地进行证券组合。

（一）证券投资组合的报酬率

证券组合的期望报酬率就是组成证券投资组合的各种投资项目的期望报酬率的加权平均数，其权数是各种投资项目在整个投资项目总额中所占比例。其公式为：

公式中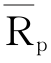为证券投资组合报期望报酬率；Wj为投资于j资产的资金占总投资额的比例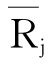；为资产j的期望报酬率；m为投资资产组合中不同投资项目的总数。

【例3-17】某投资组合由两种权重相同的证券组成，这两种证券的期望报酬率和标准离差如表3-4所示。请计算该投资组合的期望报酬率。

表3-4　A、B证券期望报酬率和标准离差

解：投资组合的期望报酬率=15%×50%+10%×50%=12.5%

（二）证券投资组合风险

在一个投资组合中，如果某一投资项目的报酬率呈上升趋势，其他投资项目的报酬率有可能上升，也有可能下降，或者不变。在统计学测算投资组合中任意两个投资项目报酬率之间变动关系的指标是协方差和相关系数，这也是投资组合风险分析中的两个核心概念。

1.协方差

协方差是一个测量投资组合中一个投资项目相对于其他投资项目风险的统计量从本质上讲，组合内各投资组合相互变化的方式影响着投资组合的整体方差，从而影响其风险。协方差的计算公式为：

我们以两个投资项目组成的投资组合来说明协方差的计算。

【例3-18】某投资组合由等权重的股票1和股票2组成，两种股票各自的报酬率如表3-5所示：

表3-5　两种股票投资报酬率数据

解：第一步，计算两种股票的平均报酬率：

第二步，计算两种股票的协方差：

协方差的正负显示了两个投资项目之间报酬率变动的方向。协方差为正值表示两种资产的报酬率呈同方向变动；协方差为负值表示两种资产的报酬率呈反方向变动，上例中股票1和股票2的报酬率就呈反向变动。协方差绝对值越大，表示这两种资产报酬率的关系越密切；协方差的绝对值越小，则这种资产报酬率的关系也越疏远。

2.相关系数

由于各方面的原因，协方差的意义很难解释，至少对于应用是如此。为了使其概念能更易于接受，可以将协方差标准化，将协方差除以两个投资方案投资报酬率的标准差之积，得出一个与协方差具有相同性质但没有量化的数。我们将这个数称为这两个投资项目的相关系数，它介于-1与+1之间。相关系数的计算公式为：

【例3-19】利用【例3-18】的数据，计算两种股票的相关系数。(www.xing528.com)

解：第一步，计算两种股票的标准离差

股票1的标准离差：

股票2的标准离差：

第二步，计算股票1和股票2的相关系数：

相关系数的正负与协方差的正负相同。所以，相关系数为正时，表示两种资产报酬率呈同方向变动，负值则意味着反方向变动。就其绝对值而言，系数值的大小与协方差大小成同向变动。相关系数总是在-1与+1之间变动，-1代表完全负相关，+1代表完全正相关，0表示不相关。

3.投资组合的总风险

投资组合的总风险由投资组合报酬率的方差和标准差来衡量。我们考虑只有A、B两种资产的组合，投资组合方差的计算公式为：

推而广之，由n种资产组合而成的投资组合的方差为：

投资组合的标准离差为：

式中，VP为投资组合的方差；δP为投资组合的标准离差；Wi为资产i在总投资中所占的比重；Wj为资产j在总投资额中所占的比重；Cov（Ri，Rj）为资产A和资产B的协方差。

【例3-20】利用表3-5中的数据和【例3-19】计算的结果，计算投资组合的方差和标准离差。

（三）风险分散化原理

在投资界有一句经典名言：“不要把所有鸡蛋放在一个篮子里”，这句话的意思是鼓励大家把资产分散投资，其内在含义是通过资产的分散化来分散风险。我们先来看一个两种证券组成的投资组合的例子。

【例3-21】假设某投资组合由A、B两种证券组成，其预期报酬率和标准离差如表3-6所示：

表3-6　A、B投资组合的预期报酬率和标准离差

我们分别按不同权重将两种证券进行组合，并分别计算投资组合的标准离差。结果如表3-7所示：

表3-7　A、B投资组合的标准离差

由上述结果可以看出，组合的标准离差总是小于标准离差的组合，说明投资组合确实能起到降低风险的作用，这就是投资风险分散化的原理。