时间价值计算：资金的复利增值和折现率

（一）一次性收付的货币时间价值的衡量

由于货币在不同时点的价值不同，货币时间价值的表现形式有两种——从现在观点看的现值（Present Value，缩写为PV）和从将来观点看的终值（Future Value，缩写为FV）。终值是指现在一定数额的货币按一定的利率计算的一定时间后的价值。现值则是指未来一定时间的特定货币按一定利率折算到现在的价值。

货币时间价值即货币运用中发生的增值额通常用利息或利息率来表示。利息的计算包括单利和复利两种形式。在单利方式下，本金能生利，而利息不能生利。所谓复利，就是不仅本金要计算利息，利息也要计算利息，即通常所说的“利滚利”。

资金的时间价值一般都是按复利的方式计算的。资金时间价值按复利计算，是建立在资金再投资这一假设基础之上的。

1.复利终值的计算

复利终值，是指一次的收或付款项经过若干期的使用后，所获得的包括本金和利息在内的未来价值。

终值的计算公式为：

式中，FVn为复利终值；PV为复利现值；i为利息率；n为计息期数。

【例3-1】某人将100元存入银行，利息率为10%，求5年后终值。

解：FV5=PV（1+i）5=100×（1+10%）5=161.05（元）

式（3-1）中的（1+i）n称为复利终值系数，可以写成（F/P，i，n），复利终值的计算公式可写成：

为了简化计算，可编制复利终值系数表，详见书后附表1，例3-1可查附表1，得知（F/P，10%，5）为1.6105，按照这个查找结果，计算终值如下：

FV5=100×（1+10%）5=100×（F/P，10%，5）=100×1.6105=161.05（元）

2.复利现值的计算

复利现值是指以后年份收到或支出资金的现在价值，可用倒求本金的方法计算。由终值求现值称为折现，在折现时使用的利息率称为折现率。

现值的计算公式可由终值的计算公式导出：

由公式FVn=PV（1+i）n可以得到

式（3-3）中的称为复利现值系数或折现系数，可以写成（P/F，i，n），则复利现值的计算公式可写为：

为了简化计算，也可以编制复利现值系数表，详见书后附表2。

【例3-2】若某人计划在3年后得到400元，利息8%，现在应存多少钱？

或查复利现值系数表计算如下：

PV=FVn（P/F，8%，3）=400×0.7938=317.52（元）

（二）等额系列收付的货币时间价值衡量

复利的终值和现值指的是一次性收（或付）款项，而年金（annuity）是指一定时期内每期相等金额的收付款项。年金具有连续性和等额性，即年金是在一定时期内每隔一段时间就必须发生一次收（或付）业务，形成一系列的同性质业务活动，而且每期发生的款项在数额上必须相等。

在经济生活中，分期等额形成的各种偿债基金、利息、租金、保险费等均表现为年金的形式。年金按付款方式，可分为普通年金（后付年金）、预付现金（先付年金）、递延年金和永续年金。其中，普通年金应用最广泛，其他几种年金均可以在普通年金的基础上推算出来。因此，一定要掌握普通年金有关的计算。

1.普通年金的终值和现值

普通年金是指每期期末有等额收付款项的年金。在现实经济生活中这种年金最为常见，故称为普通年金。年金是与复利相联系的，年金的现值和终值都是以复利的终值和现值为基础计算的。普通年金终值和现值的计算也是如此。在实际工作中，我们把普通年金终值和现值的计算简称为年金终值和现值的计算。

（1）普通年金终值。普通年金终值如同零存整取的本利和，它是一定时期内每期期末等额收付款项的复利终值之和。

假设A为年金数额，i为利息率，n为计息期数，FVAn代表年金终值。则普通年金终值的计算可以用图3-1来说明。

图3-1　普通年金终值的计算示意图

通过图3-1可知，普通年金终值的计算公式为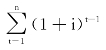：称为年金终值系数，通常写作（F/A，i，n）。

则年金终值的计算公式可写成：

为了简化计算，也可编制年金终值系数表，详见书后附表3，表中普通年金终值系数可按下列公式计算：

式（3-5）中的

【例3-3】某人5年中每年年底存入银行100元，存款利率为8%，求第5年年末年金终值。

解：FVA5=A（F/A，8%，5）=100×5.8666=586.66（元）

（2）普通年金现值。一定时期内每期期末等额的系列收付款项的现值之和叫普通年金现值，通常写作PVAn，其计算情况可用图3-2加以说明。

图3-2　普通年金现值计算示意图

由图3-2可知，年金现值的计算公式为：

式中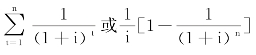，称为年金现值系数，可简写为（P/A，i，n）。普通年金现值的计算公式可写为：

为了简化计算，可先编制年金现值系数表，详见书后附表4，在编表时，年金现值系数按下列公式计算：

【例3-4】某人现在存入一笔钱，准备在以后5年中每年年末得到100元，如果利息率为10%，现在应存入多少元？

解：PVA5=A（P/A，10%，5）=100×3.7908=379.08（元）

（3）偿债基金。在普通年金终值计算中，我们是已知A来求FVAn。如果已经知道（F/A，i，n）、FVAn来求A，这就是偿债基金，即年金终值达到既定金额每年应支付的年金数额。

由于FVAn=A（F/A，i，n），所以：

其中，为偿债基金系数，记为（A/F，i，n）。它是年金终值系数的倒数。因此，可以根据年金终值系数表的倒数来确定。

【例3-5】甲公司计划5年后购置一条生产线，预计购买价格为10万元。如果利率为10%，则甲公司每年末应该提存多少准备金？

（4）资本回收值。资本回收值是指在一定时期内，分若干期回收一笔利率固定的款项，每一期应回收的等量金额。这就是说，已知年金的现值，要求以后每年应回收的本金额。

由于资本回收值是已知年金现值，求年金，因此计算资本回收值的公式可以从年金现值公式导出：

因为，PVAn=A（P/A，i，n）

【例3-6】某人取得贷款，连续等额偿还总额为10万元，贷款利率为10%，偿付期为10年，每年偿还金额为多少？

2.预付年金终值和现值

预付年金，又称完征年金或即征年金，是指在一定时期内，各期期初等额的系列收付款项。普通年金和预付年金的区别仅在于付款时间的不同。由于普通年金是最常用的，因此，年金终值和现值的系数表是按普通年金编制的，为了便于计算和查表，必须根据普通年金的计算公式，推导出预付年金的计算公式。

（1）预付年金终值。n期预付年金终值和n期普通年金终值的关系可以用图3-3加以说明。

方法1：

图3-3（A）　预付年金终值与普通年金终值关系(www.xing528.com)

方法2：

图3-3（B）　预付年金终值和普通年金终值的关系

从图3-3可以看出，根据普通年金计算预付年金终值可以采取两种方法，采用方法时，n期预付年金终值与n期普通年金终值的付款次数相同，但由于付款时间的不同，期预付年金终值比n期普通年金多计算一期利息。所以，可先求出n期普通年金终值然后再乘以（1+i）便可求出n期预付年金的终值。其计算公式为：

采用方法2时，可以根据n期预付年金终值与n+1期普通年金终值的关系推导出另一计算公式。n期预付年金与n+1期普通年金的计算期数相同，但比n+1期普通年金少付一次款，因此，只要将n+1期普通年金的终值减去一期付款额A，便可求出n期预付年金终值，计算公式为：

【例3-7】某人每年年初存入银行1 000元，银行存款利率为8%，第10年年末的本利和应为多少？

解：（1）用式（3-13）计算结果为：

XFVA10=1 000×(F/A,8%,10)×(1+8%)

=1 000×14.4866×1.08

=15 646（元）

（2）用式（3-14）计算结果为：

XFVA10=1 000×[(F/A,8%,11)-1]

=1 000×(16.6455-1)

=15 646（元）

（2）预付年金现值

n期预付年金现值与n期普通年金现值的关系，可以用图3-4加以说明。

图3-4　预付年金现值与普通年金现值的关系

从图3-4可以看出n期预付年金现值与n期普通年金现值的付款次数相同，但由于付款时间不同，在计算现值时，n期普通年金比n期预付年金多折现一期。所以，可先求出n期普通年金的现值，然后再乘以（1+i）便可求出n期预付年金的现值。其计算公式为：

此外，还可根据n期预付年金现值与n-1期普通年金现值的关系推导出另一计算公式。n期预付年金现值与n-1期普通年金现值的折现期数相同，但比n-1期普通年金多一期不用折现的付款A，因此，只要将n-1期普通年金的现值加上一期不用折现的付款额A，便可求出n期预付年金现值，计算公式为：

【例3-8】某企业租用一台设备，在10年中每年年初要支付5 000元，年利息率为8%，这些租金的现值为多少？

解：（1）用式（3-15）计算的结果为：

XPVAn=5 000×(P/A,8%,10)×(1+8%)

=5 000×6.7101×1.08

=36 235（元）

（2）用式（3-16）计算结果为：

XPVAn=5 000×[(P/A,8%,9)+1]

=5 000×(6.2469+1)

=36 235（元）

3.递延年金

递延年金是指在最初若干期没有收付款项的情况下，后面若干期有等额的系列收付款项的年金。假定最初有m期没有收付款项，后面n期每年有等额的系列收付款项，递延年金示意图如图3-5所示：

图3-5　递延年金示意图

（1）递延年金的终值。递延年金的终值与递延期无关，故计算方法和普通年金终值相同。

（2）递延年金的现值。由于递延期的存在，递延年金的现值不能按照普通年金计算现值。递延年金现值常用的计算方法有两种：

方法1：把递延年金视为n期普通年金，求出递延期末的年金现值，然后再将此现值用复利调整到第一期期初。其计算原理如图3-6所示：

图3-6　递延年金现值计算方法1

从图3-6中可以看出，先求出递延年金在n期期初（m期期末）的现值，再将其作为终值折现至m期的第一期期初，便可求出递延年金的现值。其计算公式为：

方法2：假设递延期中也有收付款项，先求出（m+n）期的年金现值，然后扣除其实际并未发生收付的递延期（m期）的年金现值，即可求出递延年金的现值。其计算原理如图3-7所示：

图3-7　递延年金现值计算方法2

从图3-7中可以看出，先求出m+n期普通年金现值，减去没有付款的前m期普通年金现值，二者之差便是延期m期的n期普通年金现值。其计算公式为：

【例3-9】某企业向银行借入一笔款项，银行贷款的年利息率为8%，银行规定前10年不需还本付息，但从第11年至第20年每年年末需偿还本息1 000元，这笔款项的现值应是多少？

解：（1）用式（3-18）计算的结果为：

V0=A(P/A,i,n)×(P/F,i,m)

=1 000×(P/A,8%,10)×(P/F,8%,10)

=1 000×6.7101×0.4632

=3 108（元）

（2）用式（3-19）计算的结果为：

V0=A[(P/A,i,n+m)-(P/A,i,m)]

=1 000×[(P/A,8%,10+10)-(P/A,8%,10)]

=1 000×(9.8181-6.7101)

=3 108（元）

4.永续年金

永续年金是指无限期支付的年金。西方有些债券为无限期债券，这些债券的利息可以视为永续年金；优先股因为有固定的股利而又无到期日，因而优先股利也可以看作永续年金。在实际生活中，可以将期限长、利率高的年金视为永续年金。

永续年金无终止时间，所以不存在终值的问题。永续年金的现值同样是通过普通年金现值的计算推导出来的：

当n→∞时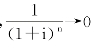，，所以永续年金现值的计算公式为：

【例3-10】某永续年金每年年底的收入为800元，利息率为8%，求该项永续年金的现值。

解：V0=800×=10 000（元）