【摘要】：投资者通过权衡一个投资项目收益率和风险的大小作出风险决策，而且会遵循最大化的原则。在期望效用理论下，我们考虑一个风险厌恶的理性投资者，他的初始财富值为W 0，有两种资产可供投资，一种是无风险资产，收益率固定为i，另一种是风险资产，收益率是随机的，为~r。
投资者通过权衡一个投资项目收益率和风险的大小作出风险决策，而且会遵循最大化的原则。
在期望效用理论下，我们考虑一个风险厌恶的理性投资者，他的初始财富值为W 0，有两种资产可供投资，一种是无风险资产，收益率固定为i，另一种是风险资产，收益率是随机的，为~r。投资者必须作出决定在初始财富W 0中有多少财富是用于投资风险资产的，又有多少是用于投资无风险资产的。用α表示投资于风险资产的财富占初始财富的比例（α≥0），~W表示期末财富总额，则期末投资者的财富总额可表示为
整理后可得
理性投资者为了追求效用最大化，必须确定α的最优值α*以使
的期望效用Eu（
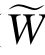）达到最大。其中，E（.）表示期望函数，u（.）为一冯诺依曼-摩根斯坦效用函数，满足u′＞0，u″≤0。
假设风险资产只会出现两种投资结果，一种比较理想，收益率达到R，另一种结果并不理想，收益率仅为r，因此可以将风险资产的收益率表示为
=
表示出现收益率为R的概率，则收益率为r的概率对应为l-p。(www.xing528.com)
如此，期末投资者持有财富的期望效用为
整理后得
分别求Eu（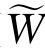
）的一阶导数和二阶导数，得
当满足最大化的条件d E/dα=0，d2E/dα2＜0时，解得α=α*为一个风险厌恶的理性投资者满足效用最大化的投资决策。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
