阿莱斯悖论及其优化方法

自从l944年冯·诺伊曼和摩根斯坦的经典巨著《对策论和经济行为》问世以来，期望效用理论就在风险决策领域一直占据主导地位，它是在带有不确定性的环境下的完全理性决策理论。期望效用理论通俗易懂，呈现标准化的逻辑严密的公理化体系，并且还容易描述个人的决策行为，比如效用函数的凹性刻画个体的风险厌恶态度，阿罗-普拉特（Arrow-Pratt）用此来衡量个体的风险厌恶程度，等等。期望效用理论以完全理性为假设前提，但是后来经济学家结合社会学、心理学等学科精心设计了大量的实验，研究发现人们的态度、偏好、行为等并不是完全理性的，他们对于风险的态度以及决策行为经常表现出违背期望效用理论。l952年，法国著名经济学家阿莱斯（Allais）提出了著名的阿莱斯悖论（Allais Paradox），对期望效用理论构成了一定的挑战。

阿莱斯设计了两组彩票选择实验，以上百个对概率论有所了解的人作为实验研究主体，让他们对以上两组彩票选择实验不带偏见地作出自己的判断。最后，实验结果显示绝大多数参加选择的人都作出了与独立性公理相反的判断，即阿莱斯得出的这个实验研究结果是违背独立性公理的，由此得出悖论，这就是所谓的阿莱斯悖论。阿莱斯设计的彩票选择实验如表4.l所示。

表4.1　阿莱斯设计的彩票选择实验

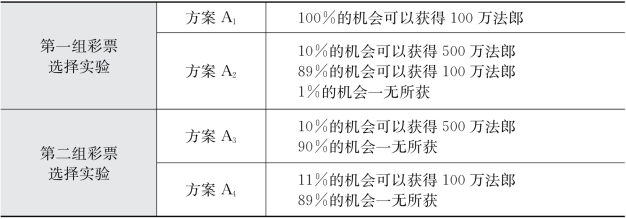
为了清楚地认清这两组彩票选择实验中四个方案的区别，我们根据上述期望效用函数公理化陈述将这四个方案化解成简单的数学形式。

令L l=（l，l，0.l l），L 2=（5，0，l0/l l），其中单位取作百万法郎。(www.xing528.com)

首先我们来分析第一组彩票选择实验。

根据公理（x，y，p）=（y，x，l-p），意味着未定产品x，y之间没有顺序的差别，由此得出L l=（l，l，0.l l）=（l，l，0.89）=A l，那么显然L l=A l；

根据公理（（x，y，p），y，q）=（x，y，pq），意味着投资者只在乎可能得到的产品向量的最终概率，至于对具体得到的过程并不关心，由此得出（L 2，l，0.l l）=（（5，0，l0/l l），l，0.l l）=（5，0，0.l），那么显然（L 2，l，0.l l）=A 2。

同理，我们再来分析第二组彩票选择实验：

根据上述表达式，显然A 4=（l，0，0.l l）=（0，l，0.89），又（L 2，0，0.l l）=（（5，0，l0/l l），l，0.l l）=（5，0，0.l）=（0，5，0.9），那么显然（L 2，0，0.l l）=A 3。

通过上述分析，看起来差别很大的这两组彩票选择实验就变得很简单。根据期望效用函数的独立性公理，方案A l，方案A 2之间和方案A 3，方案A 4之间的偏好选择问题就完全取决于决策者对l与L 2之间的选择。如果决策者认为l～L 2，那么根据独立性公理，决策者应该认为A l～A 2，A 3～A 4。也就是说符合公理化偏好假定的决策者如果在第一组彩票选择实验中选择方案A l，那么他在第二组彩票选择实验中一定会选择方案A 4。而如果决策者认为A l＞A 2，意味着l＞L 2，那么决策者肯定认为A 4＞A 3；反之，如果决策者认为A 2＞A l，意味着L 2＞l，那么决策者肯定认为A 3＞A 4。这意味着A l＞A 2只能与A 4＞A 3相容。也就是说，根据期望效用函数的理性选择理论，风险厌恶型的决策者在这两组彩票选择实验中应该选方案A l和方案A 4；而风险偏好型的决策者在这两组彩票选择实验中应该选方案A 2和方案A 3。但是阿莱斯的实验研究发现，在方案A l l和方案A 2之间，绝大多数的决策者会选择方案A l，而在方案A 3和方案A 4之间，绝大多数的决策者会选择方案A 4，连著名的经济学家和数学家萨维奇都没有例外。可以说，阿莱斯悖论是典型的风险厌恶悖论。阿莱斯最大的贡献在于指出了独立性公理是不符合实际的，但在期望效用函数的公理化体系中，独立性公理假设又恰恰是其核心与特色之处。